Třídění je jednou z nejpoužívanějších funkcí v programování. A dokončení řazení bude nějakou dobu trvat, pokud jsme nepoužili správný algoritmus.
V tomto článku budeme diskutovat o různých třídicích algoritmech.
Provedeme vás různými třídicími algoritmy při každém kroku implementace. Implementační část bude v Pythonu. Jakmile získáte algoritmus, můžete jej snadno převést do jakéhokoli jazyka. To je otázka syntaxe jazyka.
V tomto tutoriálu uvidíme různé algoritmy od nejhoršího po nejlepší. Takže se nebojte. Postupujte podle článku a implementujte je.
Pojďme se ponořit do třídicích algoritmů.
Table of Contents
Řazení vkládání
Vložení řazení je jedním z jednoduchých třídicích algoritmů. Je snadné to implementovat. A třídění pole vás bude stát více času. Nebude se ve většině případů používat pro řazení větších polí.
Algoritmus řazení vložení udržuje v daném poli seřazené a neseřazené podčásti.
Seřazená podčást obsahuje pouze první prvek na začátku procesu třídění. Vezmeme prvek z neseřazeného pole a umístíme je na správnou pozici v seřazeném podpole.
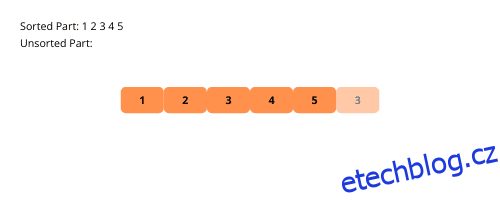
Podívejme se na vizuální ilustrace řazení vkládání krok za krokem s příkladem.
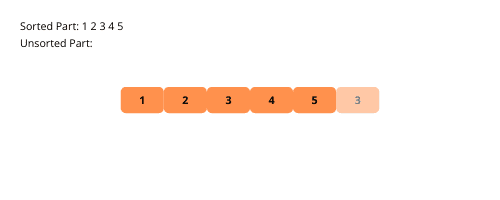
Podívejme se na kroky k implementaci řazení vložení.
- Inicializujte pole pomocí fiktivních dat (celých čísel).
- Iterujte dané pole z druhého prvku.
- Vezměte aktuální pozici a prvek ve dvou proměnných.
- Napište smyčku, která se opakuje, dokud se neobjeví první prvek pole nebo prvek, který je menší než aktuální prvek.
- Aktualizujte aktuální prvek předchozím prvkem.
- Snížení aktuální pozice.
- Zde musí smyčka dosáhnout buď začátku pole, nebo najít menší prvek, než je aktuální prvek. Nahradit prvek aktuální polohy aktuálním prvkem.
Časová složitost řazení vložení je O(n^2) a prostorová složitost, pokud O(1).
A je to; seřadili jsme dané pole. Spusťte následující kód. Doufám, že jste nainstalovali Python, pokud ne, podívejte se na instalační příručku. Případně můžete použít online kompilátor Pythonu.
def insertion_sort(arr, n): for i in range(1, n): ## current position and element current_position = i current_element = arr[i] ## iteratin until ### it reaches the first element or ### the current element is smaller than the previous element while current_position > 0 and current_element < arr[current_position - 1]: ## updating the current element with previous element arr[current_position] = arr[current_position - 1] ## moving to the previous position current_position -= 1 ## updating the current position element arr[current_position] = current_element if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] insertion_sort(arr, 9) ## printing the array print(str(arr))
Výběr Seřadit
Řazení výběru je s malým rozdílem podobné řazení vložení. Tento algoritmus také rozděluje pole na seřazené a netříděné podčásti. A pak při každé iteraci vezmeme minimální prvek z neseřazené podčásti a umístíme jej na poslední pozici seřazené podčásti.
Pro lepší pochopení si ukažme ilustraci výběru.
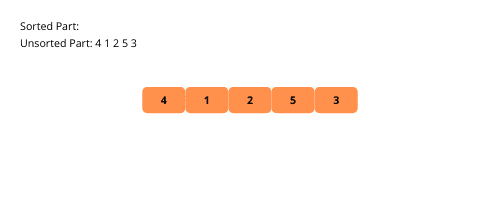
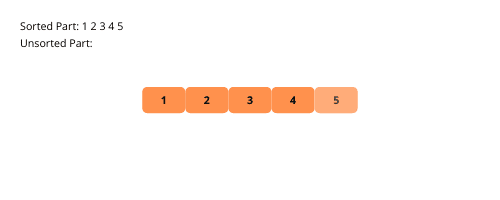
Podívejme se na kroky k implementaci řazení výběru.
- Inicializujte pole pomocí fiktivních dat (celých čísel).
- Iterujte přes dané pole.
- Udržujte index minimálního prvku.
- Napište smyčku, která iteruje od aktuálního prvku k poslednímu prvku.
- Zkontrolujte, zda je aktuální prvek menší než minimální prvek nebo ne.
- Pokud je aktuální prvek menší než minimální prvek, nahraďte index.
- Máme s sebou minimální index prvků. Zaměňte aktuální prvek za minimální prvek pomocí indexů.
Časová složitost výběru je O(n^2) a prostorová složitost, pokud O(1).
Zkuste implementovat algoritmus, protože je podobný řazení vkládání. Kód můžete vidět níže.
def selection_sort(arr, n): for i in range(n): ## to store the index of the minimum element min_element_index = i for j in range(i + 1, n): ## checking and replacing the minimum element index if arr[j] < arr[min_element_index]: min_element_index = j ## swaping the current element with minimum element arr[i], arr[min_element_index] = arr[min_element_index], arr[i] if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] selection_sort(arr, 9) ## printing the array print(str(arr))
Bublinové řazení
Bubble sort je jednoduchý algoritmus. Při každé iteraci opakovaně zaměňuje sousední prvky, dokud není dané pole seřazeno.
Iteruje pole a přesouvá aktuální prvek na další pozici, dokud nebude menší než další prvek.
Ilustrace nám pomáhají vizuálně porozumět bublinovému řazení. Pojďme se na ně podívat.
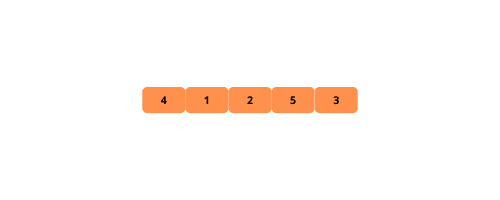
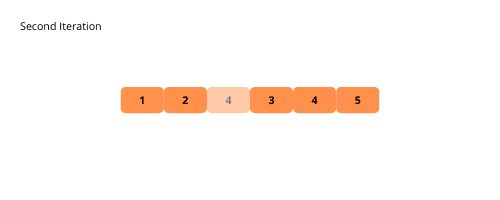
Podívejme se na kroky k implementaci bublinového řazení.
Časová složitost bublinového řazení je O(n^2) a prostorová složitost, pokud O(1).
Bublinové řazení již můžete snadno implementovat. Podívejme se na kód.
def bubble_sort(arr, n): for i in range(n): ## iterating from 0 to n-i-1 as last i elements are already sorted for j in range(n - i - 1): ## checking the next element if arr[j] > arr[j + 1]: ## swapping the adjucent elements arr[j], arr[j + 1] = arr[j + 1], arr[j] if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] bubble_sort(arr, 9) ## printing the array print(str(arr))
Sloučit třídění
Merge sort je rekurzivní algoritmus pro řazení daného pole. Je efektivnější než dříve diskutované algoritmy z hlediska časové složitosti. Sleduje přístup rozděl a panuj.
Algoritmus slučovacího řazení rozděluje pole na dvě poloviny a třídí je samostatně. Po seřazení dvou polovin pole je sloučí do jednoho seřazeného pole.
Protože se jedná o rekurzivní algoritmus, rozděluje pole, dokud se pole nestane nejjednodušším (pole s jedním prvkem), které lze seřadit.
Je čas na ilustraci. Pojďme se na to podívat.
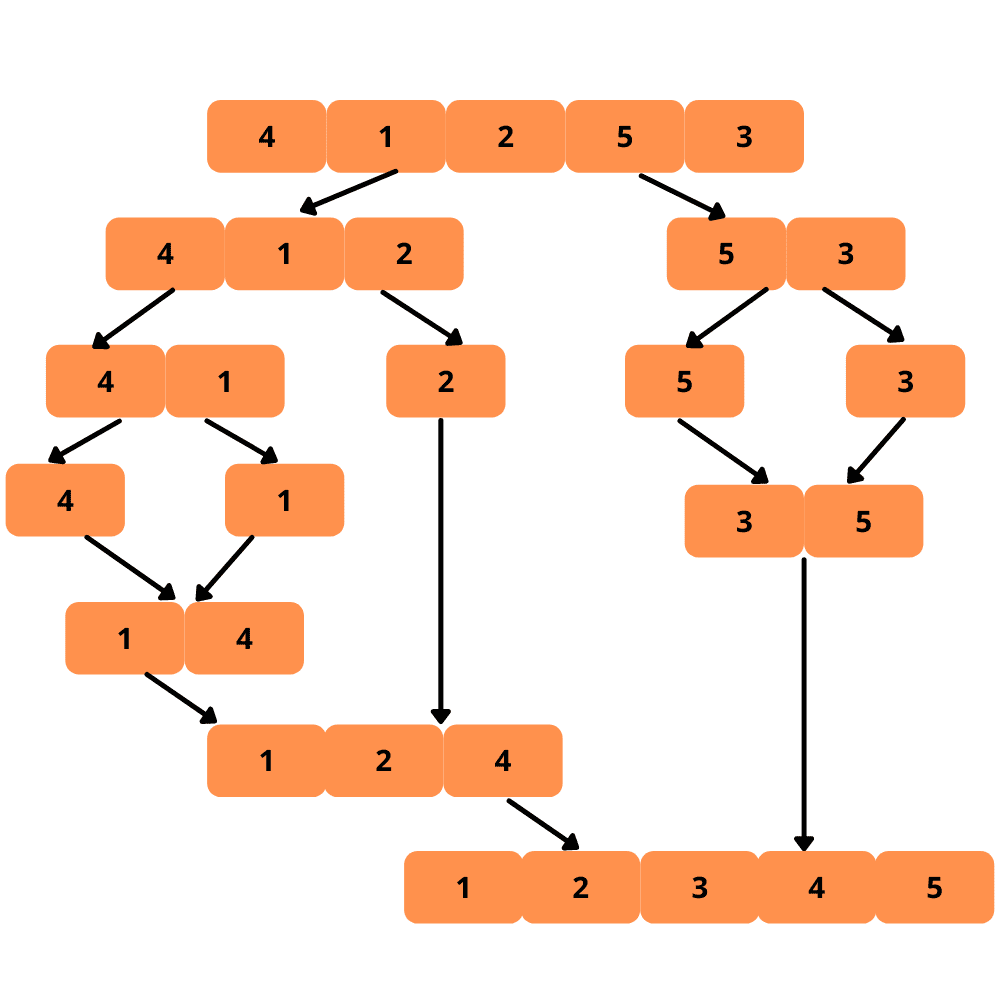
Podívejme se na kroky k implementaci řazení sloučení.
- Inicializujte pole pomocí fiktivních dat (celých čísel).
- Napište funkci nazvanou merge pro sloučení dílčích polí do jednoho seřazeného pole. Přijímá pole argumentů, levý, střední a pravý index.
- Získejte délky levého a pravého podpole pomocí daných indexů.
- Zkopírujte prvky z pole do příslušného levého a pravého pole.
- Iterujte přes dvě dílčí pole.
- Porovnejte dva prvky dílčích polí.
- Nahraďte prvek pole menším prvkem ze dvou dílčích polí pro řazení.
- Zkontrolujte, zda v obou dílčích polích nezůstaly nějaké prvky.
- Přidejte je do pole.
- Napište funkci s názvem merge_sort s polem parametrů, levým a pravým indexem.
- Pokud je levý index větší nebo roven pravému indexu, vraťte se.
- Najděte střední bod pole a rozdělte pole na dvě poloviny.
- Rekurzivně volejte merge_sort pomocí levého, pravého a středního indexu.
- Po rekurzivních voláních sloučte pole s funkcí sloučení.
Časová složitost slučovacího řazení je O(nlogn) a prostorová složitost, pokud O(1).
To je vše pro implementaci algoritmu řazení sloučení. Zkontrolujte kód níže.
def merge(arr, left_index, mid_index, right_index): ## left and right arrays left_array = arr[left_index:mid_index+1] right_array = arr[mid_index+1:right_index+1] ## getting the left and right array lengths left_array_length = mid_index - left_index + 1 right_array_length = right_index - mid_index ## indexes for merging two arrays i = j = 0 ## index for array elements replacement k = left_index ## iterating over the two sub-arrays while i < left_array_length and j < right_array_length: ## comapring the elements from left and right arrays if left_array[i] < right_array[j]: arr[k] = left_array[i] i += 1 else: arr[k] = right_array[j] j += 1 k += 1 ## adding remaining elements from the left and right arrays while i < left_array_length: arr[k] = left_array[i] i += 1 k += 1 while j < right_array_length: j += 1 k += 1 def merge_sort(arr, left_index, right_index): ## base case for recursive function if left_index >= right_index: return ## finding the middle index mid_index = (left_index + right_index) // 2 ## recursive calls merge_sort(arr, left_index, mid_index) merge_sort(arr, mid_index + 1, right_index) ## merging the two sub-arrays merge(arr, left_index, mid_index, right_index) if __name__ == '__main__': ## array initialization arr = [3, 4, 7, 8, 1, 9, 5, 2, 6] merge_sort(arr, 0, 8) ## printing the array print(str(arr))
Závěr
Existuje mnoho dalších třídicích algoritmů, ale výše jsou uvedeny některé z často používaných. Doufám, že se vám učení třídění líbilo.
Dále se dozvíte o vyhledávacích algoritmech.
Veselé kódování 🙂 👨💻