Od počátků konceptu kvantového počítače v roce 1980 do dnešních dnů zažil obor kvantových výpočtů enormní růst, zejména během posledního desetiletí. Spousta firem se aktivně věnuje vývoji kvantových počítačů.
Pro mnoho z nás může být pochopení kvantových počítačů komplikované, a navíc mnohé z dostupných informací postrádají důležité detaily.
Cílem tohoto článku je vše srozumitelně objasnit. Po jeho přečtení byste měli získat komplexní přehled o kvantovém počítání, jeho různých typech, principech fungování, algoritmech, modelech, přístupech, výzvách a aplikačních možnostech.
Co jsou kvantové počítače?
Kvantové počítače řeší problémy odlišným způsobem než běžné počítače, které budeme dále označovat jako klasické počítače.
Kvantové počítače nabízejí oproti klasickým počítačům výhody v řešení specifických problémů, a to díky jejich schopnosti existovat v obrovském množství stavů současně, zatímco klasické počítače mohou v daný moment zaujímat pouze jeden stav.
Zdroj obrázku: IBM
Abyste porozuměli principu fungování kvantových počítačů, je třeba pochopit tři klíčové koncepty: superpozici, provázanost a interferenci.
Základním stavebním kamenem běžného počítače jsou bity, zatímco pro kvantový počítač jsou to kvantové bity, zkráceně qubity. Tyto fungují na zcela odlišných principech.
Klasický bit je jako spínač, který může nabývat hodnoty 0 nebo 1, což je vám pravděpodobně známo jako binární informace. Pokud bit změříme, získáme zpět jeho aktuální stav. U qubitů tomu tak ale není. Qubit je mnohem složitější.
Superpozice
Pro názornost si qubit můžete představit jako šipku směřující v trojrozměrném prostoru. Pokud směřuje nahoru, je ve stavu 1, pokud směřuje dolů, je ve stavu 0, podobně jako klasický bit. Avšak má i možnost být ve stavu nazývaném superpozice, kdy šipka směřuje libovolným jiným směrem.
Tento stav superpozice je kombinací stavů 0 a 1.
Pokud qubit změříte, výsledkem bude stále buď 1, nebo 0, avšak pravděpodobnost, kterou z těchto hodnot získáte, závisí na orientaci šipky.
Pokud šipka směřuje spíše nahoru, je pravděpodobnější, že získáte 1 než 0, a naopak. Pokud směřuje přesně na rovník, získáte oba stavy s 50% pravděpodobností.
Tímto je objasněn efekt superpozice. Nyní se podíváme na provázanost.
Provázanost
V klasických počítačích jsou bity na sobě zcela nezávislé. Stav jednoho bitu neovlivňuje stav ostatních bitů. V kvantových počítačích však mohou být qubity vzájemně provázané, což znamená, že se společně stávají součástí jednoho velkého kvantového stavu.
Podívejme se například na dva qubity, z nichž každý je v jiném stavu superpozice, ale dosud nejsou provázané. Vedle nich vidíte pravděpodobnosti, které jsou na sobě nezávislé.
Pokud je ale provážeme, musíme tyto nezávislé pravděpodobnosti zahodit a vypočítat rozložení pravděpodobností všech možných stavů, které můžeme získat. A to buď 00, 01, 10 nebo 11.
Důležité je, že jakmile jsou qubity provázané, změna orientace šipky u jednoho qubitu ovlivní rozdělení pravděpodobností celého systému. Qubity již nejsou nezávislé, ale stávají se součástí stejného velkého stavu.
Toto platí bez ohledu na to, kolik qubitů máte. Je také patrné, že pro jeden qubit máte rozdělení pravděpodobnosti do 2 stavů.
Se dvěma qubity máte rozdělení pravděpodobnosti rozděleno do čtyř stavů. Pro tři qubity je to distribuce přes 8 stavů. Toto číslo se neustále zdvojnásobuje s každým přidaným qubitem.
Obecně platí, že kvantový počítač s n qubity může být v kombinaci 2n stavů. Toto je klíčový rozdíl mezi klasickými a kvantovými počítači.
Klasické počítače mohou být v jakémkoli stavu, avšak vždy pouze v jednom stavu, zatímco kvantové počítače mohou být v superpozici všech těchto stavů současně.
Možná vás napadne, jak může být stav superpozice v počítači užitečný. K tomu potřebujeme poslední komponentu: interferenci.
Interference
K objasnění účinku interference se vrátíme k obrázku qubitu, který se odborně nazývá Blochova koule. Qubit takto ve skutečnosti nevypadá; je to pouze názorný způsob vizualizace stavu qubitu.
Ve skutečnosti je stav qubitu popsán abstraktnější entitou, známou jako kvantová vlnová funkce. Vlnové funkce jsou základním matematickým popisem všeho v kvantové mechanice.
Když máte mnoho qubitů provázaných, jejich vlnové funkce se sčítají do celkové vlnové funkce, která popisuje stav kvantového počítače.
Toto sčítání vlnových funkcí je interferencí. Stejně jako u vlnění vody, když vlny sčítáme dohromady, mohou konstruktivně interferovat a zesilovat se, nebo destruktivně interferovat a navzájem se rušit.
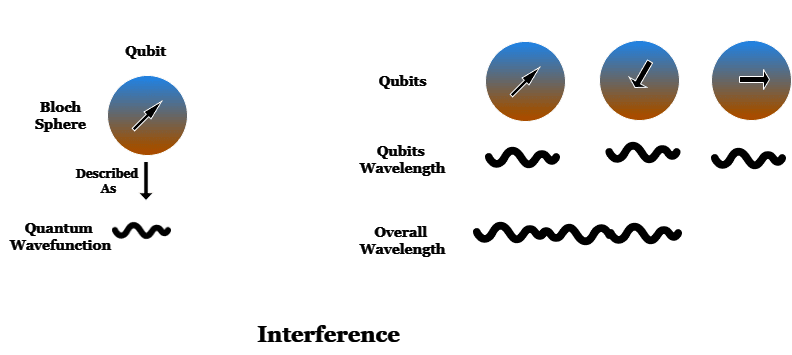
Celková vlnová funkce kvantového počítače určuje pravděpodobnosti různých stavů. Změnou stavů různých qubitů můžeme ovlivnit pravděpodobnost, že při měření kvantového počítače budou odhaleny různé stavy.
Pamatujte, že i když kvantový počítač může být v superpozici milionů stavů najednou, při měření vždy získáme pouze jeden stav.
Při řešení výpočetního problému na kvantovém počítači musíte pomocí konstruktivní interference zvýšit pravděpodobnost správné odpovědi a pomocí destruktivní interference snížit pravděpodobnost nesprávných odpovědí. Tím zajistíte, že při měření získáte správný výsledek.
Kvantové algoritmy
Jak toho docílit, je otázkou kvantových algoritmů. Celá motivace kvantových počítačů spočívá v tom, že teoreticky existuje spousta problémů, které lze efektivně řešit na kvantovém počítači, zatímco na klasickém počítači jsou považovány za neřešitelné.
Pojďme se na ně podívat. Existuje mnoho kvantových algoritmů, a to příliš mnoho na to, aby se daly v tomto článku popsat. Zaměříme se proto pouze na ten nejznámější a historicky nejdůležitější: Shorův algoritmus.
#1. Shorův algoritmus
Pokud máte dvě velká čísla a vynásobíte je, existuje velmi rychlý a efektivní klasický algoritmus, jak najít výsledek. Pokud ale začnete s výsledkem a zeptáte se, jaká jsou původní čísla, která se násobí, abyste získali tento výsledek, je to mnohem obtížnější.
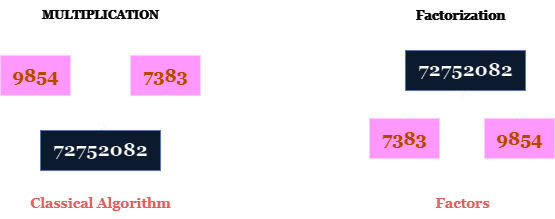
Tomuto se říká faktorizace, a čísla, ze kterých se skládá, jsou faktory. Důvodem, proč je tak těžké tyto faktory najít, je, že prostor pro hledání možných faktorů je tak obrovský a neexistuje žádný efektivní klasický algoritmus pro hledání faktorů velkých čísel.
Z tohoto důvodu využíváme této matematické vlastnosti pro šifrování na internetu: zabezpečené webové stránky, e-maily a bankovní účty. Pokud znáte tyto faktory, můžete informace snadno dešifrovat. Pokud je však neznáte, musíte je nejprve najít, což je neřešitelné i pro ty nejvýkonnější počítače na světě.
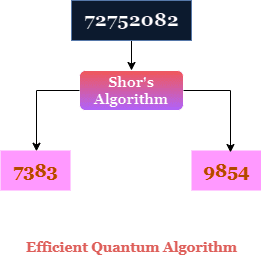
Proto v roce 1994, když Peter Shor publikoval rychlý kvantový algoritmus, který dokázal efektivně najít faktory velkých celých čísel, vyvolalo to velký ohlas.
Tehdy mnoho lidí začalo brát myšlenku kvantových počítačů vážně. Byla to první aplikace řešící problém reálného světa s potenciálně obrovskými bezpečnostními důsledky.
Když ale mluvím o „rychlém“ kvantovém algoritmu, jak rychlý je a o kolik rychlejší by byl oproti klasickému počítači? Abychom tyto otázky zodpověděli, musíme se krátce podívat do světa kvantové teorie složitosti.
Kvantová teorie složitosti
Kvantová teorie složitosti je podobor teorie výpočetní složitosti, která se zabývá kategorizací algoritmů a jejich řazením do přihrádek podle toho, jak dobře fungují na počítačích.
Klasifikace je určena rostoucí úrovní obtížnosti řešení problému, jak se jeho velikost zvětšuje. Jakýkoli problém v „P“ boxu pro klasické počítače je snadno řešitelný. Vše mimo tento box značí, že nemáme efektivní klasické algoritmy, které by tyto problémy řešily. Faktorizace velkých čísel je jedním z nich.
Existuje však kruh „BQP“, který je efektivní pro kvantový počítač, ale ne pro klasický počítač. Jedná se o problémy, které budou kvantové počítače řešit lépe než klasické počítače.
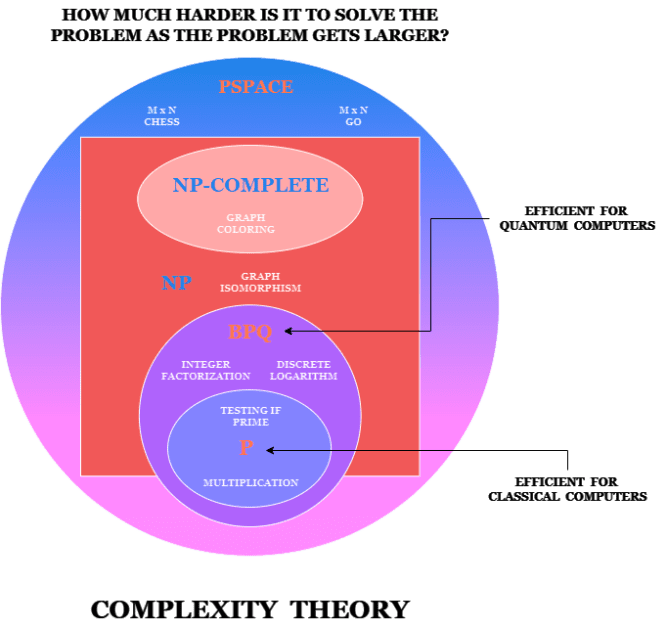
Jak jsem zmínil, teorie složitosti se zaměřuje na to, jak obtížné je vyřešit problém, pokud se jeho velikost zvětšuje. Pokud tedy faktorizujete číslo s 8 číslicemi a poté přidáte další číslici, o kolik těžší bude faktorizovat nové číslo ve srovnání se starým? Bude to dvakrát těžší?
Exponenciálně těžší? A jaký je trend, když přidáváte další a další číslice? Tomu se říká složitost nebo škálování. U faktorizace je to exponenciální.
Cokoli s N v exponentu je exponenciálně obtížné. Tyto exponenciální problémy vás zničí, pokud se problémy zvětší. Ve světě informatiky si můžete získat respekt a slávu, pokud najdete lepší algoritmus k řešení těch nejtěžších problémů.
Příkladem toho byl Shorův algoritmus, který využil speciálních vlastností kvantových počítačů k vytvoření algoritmu, který by mohl řešit celočíselnou faktorizaci s mnohem lepším škálováním než nejlepší klasický algoritmus.
Nejlepší klasický algoritmus je exponenciální, zatímco Shorův algoritmus je polynomiální. To je obrovský posun ve světě teorie složitosti a informatiky obecně, protože mění neřešitelný problém na řešitelný.
Vyřešeno, tedy pokud máte funkční kvantový počítač, na kterém lidé pracují. Nemusíte se ale zatím obávat o bezpečnost svého bankovního účtu, protože dnešní kvantové počítače zatím nejsou schopny spustit Shorův algoritmus na velkých číslech.
IBM Quantum
K tomu by potřebovali asi mnoho qubitů. Zatím nejpokročilejší univerzální kvantové počítače mají kolem 433.
Lidé také pracují na tzv. postkvantových šifrovacích schématech, které nevyužívají celočíselnou faktorizaci. Zde může pomoci i další technologie ze světa kvantové fyziky, kryptografické schéma známé jako kvantová kryptografie.
Toto byl pouze jeden kvantový algoritmus, ale je jich mnohem více, každý s jinou mírou zrychlení.
#2. Groverův algoritmus
Dalším pozoruhodným příkladem je Groverův algoritmus, který dokáže prohledávat nestrukturované seznamy dat rychleji než nejlepší klasický algoritmus.
Zde bychom si ale měli dát pozor, abychom klasické počítače nepodceňovali. Jsou to velmi všestranná zařízení a nelze říci, že by někdo nemohl objevit velmi chytrý klasický algoritmus, který by dokázal efektivněji vyřešit nejtěžší problémy, jako je faktorizace celých čísel.
Lidé si myslí, že je to velmi nepravděpodobné, ale není to vyloučeno. Existují i problémy, o kterých můžeme dokázat, že je nelze vyřešit na klasických počítačích. Jedná se o problémy neřešitelné, jako je problém zastavení. Ty nelze vyřešit ani na kvantovém počítači.
Z výpočetního hlediska jsou klasické a kvantové počítače navzájem ekvivalentní. Všechny rozdíly plynou z algoritmů, které mohou spouštět. Můžete dokonce simulovat kvantový počítač na klasickém počítači, a naopak.
Simulace kvantového počítače na klasickém počítači se s rostoucím počtem simulovaných qubitů stává exponenciálně náročnější.
Je tomu tak proto, že klasické počítače se snaží simulovat kvantové systémy. Protože kvantové počítače jsou již kvantové systémy, tento problém nemají. To mě přivádí k mé oblíbené aplikaci kvantových počítačů: kvantové simulaci.
#3. Kvantová simulace
Kvantová simulace pomocí počítače simuluje například chemické reakce nebo chování elektronů v různých materiálech. Zde mají kvantové počítače také exponenciální zrychlení oproti klasickým počítačům, protože klasické počítače se snaží simulovat kvantové systémy.
Simulovat kvantové systémy, i s velmi malým počtem částic, je však obtížné i na těch nejvýkonnějších superpočítačích na světě. Zatím to neumíme ani na kvantových počítačích, ale jak budou dozrávat, hlavním cílem je simulovat větší a větší kvantové systémy.
Zahrnují oblasti, jako je chování exotických materiálů při nízkých teplotách, pochopení, co dělá některé materiály supravodivými, nebo studium důležitých chemických reakcí za účelem zlepšení jejich účinnosti. Například snaha vyrábět hnojiva způsobem, který uvolňuje mnohem méně oxidu uhličitého, protože výroba hnojiv přispívá přibližně 2% celosvětových emisí uhlíku.
Můžete se dozvědět o simulaci kvantové chemie do hloubky.
Kvantová simulace
Další potenciální aplikace kvantové simulace zahrnují vylepšení solárních panelů, baterií a vývoj nových léků, chemikálií nebo materiálů pro letectví a kosmonautiku.
Obecně by kvantová simulace znamenala, že bychom byli schopni rychle prototypovat mnoho různých materiálů uvnitř kvantového počítače a testovat všechny jejich fyzikální parametry, místo toho, abychom je museli fyzicky vyrábět a testovat v laboratoři. Jedná se o mnohem náročnější a dražší proces.
To má potenciál výrazně urychlit procesy a vést k podstatným úsporám času a nákladů. Stojí to za to. Jedná se o problémy, pro které by se kvantové počítače hodily.
Modely kvantových počítačů
Ve světě kvantových počítačů existuje široká škála přístupů k transformaci různých typů kvantových systémů na kvantové počítače. Jsou zde dvě úrovně, které musím zmínit.
Model obvodu
V modelu obvodu mají qubity interakci pomocí speciálních bran, které manipulují s několika qubity najednou a mění jejich stavy. Tyto brány jsou uspořádány do určitého pořadí, aby vytvořily kvantový algoritmus. Nakonec se qubity změří, aby se získala potřebná odpověď.
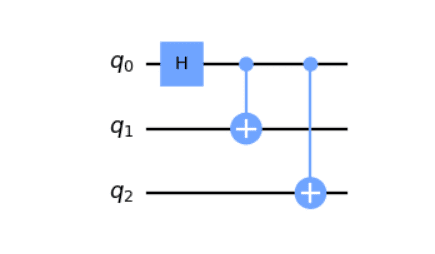Kredit obrázku: qiskit
Adiabatické kvantové počítání
V adiabatickém kvantovém počítání využíváte jedno ze základních fyzikálních chování. Skutečnost, že každý systém ve fyzice se vždy pohybuje směrem k minimálnímu energetickému stavu. Adiabatické kvantové výpočty fungují tak, že problémy rámují tak, že nejnižší energetický stav kvantového systému představuje řešení.
Kvantové žíhání
Kvantové žíhání není univerzální kvantové výpočetní schéma, ale funguje na stejném principu jako adiabatické kvantové počítání. Systém hledá minimální energetický stav dané energetické krajiny.
Topologické kvantové výpočty
V tomto přístupu jsou qubity sestaveny z entity ve fyzice, která se jmenuje Majorana kvazičástice s nulovým režimem. Jedná se o typ neabelovského anyonu. Předpokládá se, že tyto kvazičástice budou stabilnější díky jejich vzájemnému fyzickému oddělení.
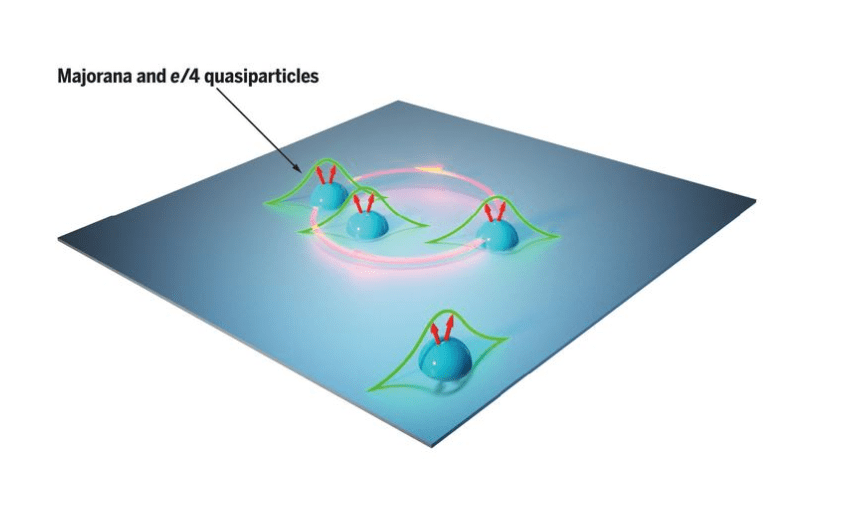Image Credit Civilsdaily
Výzvy ve stavebnictví
Bez ohledu na přístup, všichni čelí podobným překážkám, na které se nejprve musíme podívat.
- Dekoherence: Je skutečně obtížné ovládat kvantové systémy. Pokud dojde k nepatrné interakci s vnějším světem, informace začnou unikat. Tomu se říká dekoherence. Vaše qubity jsou vyrobeny z fyzických materiálů a k jejich ovládání a měření budete potřebovat další fyzické věci. Vaše qubity se zapletou do všeho, co mohou. Musíte své qubity navrhnout velmi pečlivě, abyste je ochránili před zapletením do okolí.
- Hluk: Své qubity musíte chránit před jakýmkoli druhem hluku, jako je kosmické záření, radiace, tepelná energie nebo škodlivé částice. Určitá míra dekoherence a šumu je nevyhnutelná v jakémkoli fyzikálním systému a nelze ji zcela odstranit.
- Škálovatelnost: Pro každý qubit potřebujete spoustu drátů, abyste s ním mohli manipulovat a měřit jej. Jak přidáváte další qubity, potřebná infrastruktura roste lineárně, což představuje značnou technickou výzvu. Jakýkoli návrh kvantového počítače musí najít způsob, jak efektivně proplétat, ovládat a měřit všechny tyto qubity, jak se zvětšují.
- Kvantová korekce chyb: Kvantová korekce chyb je schéma opravy chyb, které vytváří kvantové počítače odolné proti chybám pomocí mnoha provázaných qubitů dohromady. Ty představují jeden qubit bez šumu. K vytvoření jediného qubitu odolného proti chybám je potřeba velké množství fyzických qubitů.
Fyzické realizace
Existuje obrovská škála různých fyzických implementací kvantových počítačů, protože existuje tolik různých kvantových systémů, ze kterých byste je mohli potenciálně postavit. Zde jsou některé z nejpoužívanějších a nejúspěšnějších přístupů:
- Supravodivé kvantové počítače: Supravodivé qubity jsou v současnosti nejoblíbenějším přístupem. Tyto qubity jsou vyrobeny ze supravodivých drátů s přerušením v supravodiči, které se nazývá Josephsonův přechod. Nejoblíbenějším typem supravodivého qubitu je transmon.
- Quantum Dot Kvantové počítače: Qubity jsou vyrobeny z elektronů nebo skupin elektronů. Dvouúrovňový systém je zakódován do rotace nebo náboje elektronů. Tyto qubity jsou vyrobeny z polovodičů, jako je křemík.
- Lineární optické kvantové výpočty: Optické kvantové počítače používají fotony světla jako qubity. Pracují s těmito qubity pomocí optických prvků, jako jsou zrcadla, vlnové desky a interferometry.
- Kvantové počítače v pasti iontů: Nabité atomy se používají jako qubity. Tyto atomy jsou ionizované a chybí jim elektron. Dvouúrovňový stav, který kóduje qubit, jsou specifické energetické hladiny atomu. Ty se dají manipulovat nebo měřit pomocí mikrovln nebo laserových paprsků.
- Color Center nebo Nitrogen Vacancy Quantum Computers: Tyto qubity jsou vyrobeny z atomů uložených v materiálech, jako je dusík v diamantu nebo karbidu křemíku. Jsou vytvořeny pomocí jaderných spinů vložených atomů. Ty jsou zapleteny s elektrony.
- Neutrální atomy v optických mřížkách: Tento přístup zachycuje neutrální atomy do optické mřížky, což je zkřížené uspořádání laserových paprsků. Dvouúrovňovým systémem pro qubity může být hyperjemná energetická hladina atomu nebo excitované stavy.
Toto jsou některé z klíčových přístupů k budování kvantových počítačů, z nichž každý má své vlastní jedinečné vlastnosti a výzvy. Kvantové výpočty se rychle mění a výběr správného přístupu je klíčový pro budoucí úspěch.
Aplikace kvantových počítačů
- Kvantová simulace: Kvantové počítače mají potenciál simulovat komplexní kvantové systémy, což umožňuje studovat chemické reakce, chování elektronů v materiálech a různé fyzikální parametry. To má využití při zlepšování solárních panelů, baterií, vývoji léků, leteckých materiálů a dalších.
- Kvantové algoritmy: Algoritmy jako Shorův algoritmus a Groverův algoritmus mohou řešit problémy, které jsou považovány za neřešitelné pro klasické počítače. Ty mají aplikace v kryptografii, optimalizaci komplexních systémů, strojovém učení a AI.
- Kybernetická bezpečnost: Kvantové počítače představují hrozbu pro klasické šifrovací systémy. Mohou však také přispět ke kybernetické bezpečnosti prostřednictvím vývoje kvantově odolných šifrovacích schémat. Kvantová kryptografie, obor související s kvantovými výpočty, může zvýšit bezpečnost.
- Problémy s optimalizací: Kvantové počítače mohou řešit komplexní problémy s optimalizací efektivněji než klasické počítače. To má aplikace v různých průmyslových odvětvích, od řízení dodavatelského řetězce až po finanční modelování.
- Předpověď počasí a změna klimatu: I když to v článku není úplně popsáno, kvantové počítače by mohly potenciálně zlepšit modely předpovědi počasí a pomoci řešit problémy související se změnou klimatu. Toto je oblast, která může v budoucnu těžit z kvantových počítačů.
- Kvantová kryptografie: Kvantová kryptografie zvyšuje bezpečnost dat pomocí kvantových principů pro bezpečnou komunikaci. V době rostoucích kybernetických hrozeb je to zásadní.
Nyní musíme být trochu opatrní ohledně potenciálu nadšení, protože mnoho tvrzení o tom, k čemu budou kvantové počítače dobré, pochází od lidí, kteří aktivně sbírají peníze na jejich stavbu.
Můj názor je takový, že historicky, když se objevila nová technologie, lidé té doby nejsou nejlepší v tom, aby byli schopni říct, k čemu bude použita.
Například lidem, kteří vynalezli první počítače, se nikdy nesnilo o internetu a všech věcech na něm. To bude pravděpodobně stejné pro kvantové počítače.
Závěrečné myšlenky
Kvantové počítače se každým dnem zlepšují, a přestože je zatím nemůžeme používat v každodenním životě, mají potenciál pro praktické aplikace v budoucnu.
V tomto článku jsem diskutoval o různých aspektech kvantových počítačů, včetně jejich základních pojmů, jako je superpozice, provázanost a interference.
Poté jsme prozkoumali kvantové algoritmy, včetně Shorova algoritmu a Groverova algoritmu. Také jsme se ponořili do teorie kvantové složitosti a různých modelů kvantových počítačů.
Následně jsem se věnoval výzvám a problémům praktické implementace spojeným s kvantovým počítáním. Nakonec jsme prozkoumali širokou škálu potenciálních aplikací pro kvantové počítače.
Dále si také můžete přečíst o Quantum Computing FAQ.