Procentuální odchylka v datovém souboru reprezentuje rozdíl mezi přesnými a aproximovanými hodnotami, vztažený k původní hodnotě. Tato odchylka je vyjádřena v procentech, tedy násobena stem.
Procentuální odchylku lze vyjádřit jako absolutní nebo relativní chybu. K odchylkám dochází v důsledku nepřesnosti měřicích nástrojů, chyb výpočtů, chyb při měření samotném nebo vlivem okolních podmínek.
Hodnota procentuální odchylky nám pomáhá posoudit, jak významné jsou naše chyby během analýzy. Nižší procentuální odchylky signalizují, že se blížíme původní hodnotě, zatímco vyšší procentuální odchylky naznačují značnou nesrovnalost mezi skutečnou a aproximovanou hodnotou.
Například odchylka 2 % by značila velmi těsný výsledek vůči původní hodnotě, zatímco odchylka 56 % by poukazovala na velký rozdíl mezi skutečnou a přibližnou hodnotou.
Chyby měření jsou běžné, protože při měření se mohou ruce chvět, přístroje mohou být vadné nebo materiál nemusí být zcela přesný.
Jak se počítá procentuální odchylka
Pro výpočet procentuální odchylky potřebujeme dvě hodnoty: přesnou hodnotu a přibližnou hodnotu. Rozdíl mezi těmito hodnotami se vydělí původní hodnotou. Protože procentuální odchylka se vyjadřuje v procentech, výsledek se ještě vynásobí 100. Jinými slovy, procentuální odchylka je relativní chyba násobená stem.
Procentuální odchylka = [(Skutečná hodnota – Očekávaná hodnota) / Očekávaná hodnota] × 100
Složky vzorce
Skutečná hodnota: Skutečná hodnota je číselná hodnota naměřená během experimentu. V ideálním případě by se tato hodnota měla zaznamenat, ale z různých důvodů se může lišit. Představuje standardní hodnotu, která se obvykle používá pro výpočty.
Očekávaná hodnota: Očekávaná hodnota je hodnota, která byla zaznamenána během měření. Kvůli různým chybám se tato hodnota často liší od skutečné hodnoty. Chyby mohou být způsobeny chybami přístrojů, nepřesnostmi měření nebo vlivem okolních faktorů, jako je teplota či stav měřicích pomůcek.
Příklady
Příklad 1
Chlapec změřil plochu trojúhelníku a zjistil hodnotu 462 cm². Skutečná plocha však je 465 cm². Vypočítejte procentuální odchylku.
Řešení
Naměřená plocha = 462 cm²
Skutečná plocha = 465 cm²
Výpočet
Rozdíl skutečné a naměřené plochy: 465 – 462 = 3
Chyba měření je tedy 3.
Chyba vydělena skutečnou hodnotou: 3 / 465 = 0,00645
Výsledek vynásobený 100: 0,00645 × 100 = 0,64 %
Procentuální odchylka při výpočtu plochy trojúhelníku je tedy 0,64 %.
Příklad 2
Řekněme, že jste organizovali večírek a odhadovali jste účast 20 lidí, ale nakonec dorazilo jen 18 lidí. Vypočítejte procentuální odchylku ve vašem odhadu.
Řešení
Původní odhad počtu lidí = 20
Počet přítomných = 18
Výpočet
Rozdíl skutečného a konečného počtu: 20 – 18 = 2
Chyba je tedy 2.
Chyba vydělena skutečnou hodnotou: 2 / 20 = 0,1
Výsledek vynásobený 100: 0,1 × 100 = 10 %
Procentuální odchylka v odhadu počtu hostů je tedy 10 %.
Příklad 3
Předpokládejme, že jste provedli experiment k určení bodu varu vody a při experimentu jste zjistili, že je 102 °C. Skutečný bod varu vody je 100 °C.
Řešení
Skutečný bod varu vody = 100 °C
Naměřený bod varu vody = 102 °C
Výpočet
Rozdíl mezi skutečnou a vypočtenou hodnotou: 100 – 102 = -2 °C (procentuální odchylka nemůže být záporná, proto bereme absolutní hodnotu, tedy 2 °C).
Chyba je tedy 2.
Chyba vydělena skutečnou hodnotou: 2 / 100 = 0,02
Výsledek vynásobený 100: 0,02 × 100 = 2 %
Procentuální odchylka měření bodu varu vody je tedy 2 %.
Praktické scénáře, kde má procentuální odchylka význam
- Procentuální odchylka je důležitá, protože vám pomáhá posoudit, zda byl váš úkol dokončen s dostatečnou přesností. Upozorňuje na případné chyby.
- Procentuální odchylka je užitečná v laboratorních postupech a velkých průmyslových odvětvích, kde není prostor pro ani sebemenší chybu.
- Procento odchylky se také používá při hromadné výrobě, kde nesmí docházet k chybám.
- Vědecké laboratoře procentuální odchylku využívají kriticky.
Procentuální odchylka vs. absolutní chyba
Absolutní chyba měření je rozdíl mezi skutečnými a naměřenými hodnotami. Jednotka absolutní chyby je stejná jako jednotka vstupní hodnoty.
Příklad
Řekněme, že jste si chtěli koupit 2 kg manga, ale prodavač navážil 1,98 kg. Absolutní chyba je v tomto případě 2 – 1,98 = 0,02 kg.
Naproti tomu, procentuální odchylka se vypočítá tak, že absolutní chyba se vydělí původní hodnotou a výsledek se vynásobí 100. Procentuální odchylka je bezrozměrná veličina.
V předchozím příkladu je absolutní chyba 0,02 kg.
Pro výpočet procentuální odchylky vydělíme 0,02 kg hodnotou 2 kg.
0,02 / 2 = 0,01
Procentuální odchylka je v tomto případě 0,01 × 100 = 1 %.
Procentuální odchylka vs. relativní chyba
Relativní chyba v jakémkoli výpočtu je absolutní chyba dělená skutečnou hodnotou. Procentuální odchylka je tedy rozdíl mezi skutečnou a naměřenou hodnotou dělený skutečnou hodnotou.
Příklad
Předpověď počasí uváděla dnešní teplotu 38 °C. Teplota však vystoupala na 42 °C.
Nejdříve najdeme rozdíl mezi těmito dvěma čísly, tedy mezi očekávanou a skutečnou hodnotou.
42 °C – 38 °C = 4 °C
Pro výpočet relativní chyby vydělíme tento rozdíl skutečnou hodnotou, tj. 42 °C.
4 / 42 = 0,0952
Procentuální odchylka je relativní chyba vynásobená 100.
V uvedeném příkladu bude procentuální odchylka 0,0952 × 100 = 9,52 %.
Jak vidíte, je poměrně snadné vypočítat procentuální, relativní i absolutní chybu.
Výpočet procentuální odchylky si můžete usnadnit pomocí online kalkulaček. Už se nemusíte ptát, jak vypočítat procentuální odchylku, protože tyto kalkulačky to udělají za vás.
Nástroje pro výpočet odchylek
#1. Kalkulačka Calculator Soup
Calculator Soup vám pomůže vypočítat procentuální odchylku mezi experimentální a skutečnou hodnotou. Stačí zadat hodnoty a počkat na výsledky. Kalkulačka provede všechny výpočty sama a poskytne přesné výsledky.
Webová stránka má dva sloupce, kam zadáte hodnoty a kalkulačka provede zbytek.
#2. Calculator.net
Calculator.net má dva sloupce pro zadání skutečných a odhadovaných hodnot, zbytek výpočtů necháte na kalkulačce. To je užitečné, když máte k dispozici velké množství dat, pro které chcete spočítat procentuální odchylku a nemáte čas na ruční výpočty. Kalkulačka zjednoduší proces a poskytne vám odpověď bez prodlení.
Procentuální odchylky jsou nevyhnutelné. Můžete pouze snížit jejich hodnotu, ale nikdy se nestane, že by procentuální odchylka klesla na nulu. Může se nule blížit, ale nikdy to nebude přesná nula.
#3. Good Calculators
Mnoho online kalkulaček vám pomůže při řešení problémů s procentuální odchylkou. Jednou z nejužitečnějších je Good Calculators. Do této kalkulačky jednoduše zadáte odhadovanou a původní hodnotu a automaticky se zobrazí výsledky.
Ušetříte si tak zdlouhavé výpočty a čas. Komplexní výpočty lze vyřešit během několika sekund, což vám ušetří spoustu času.
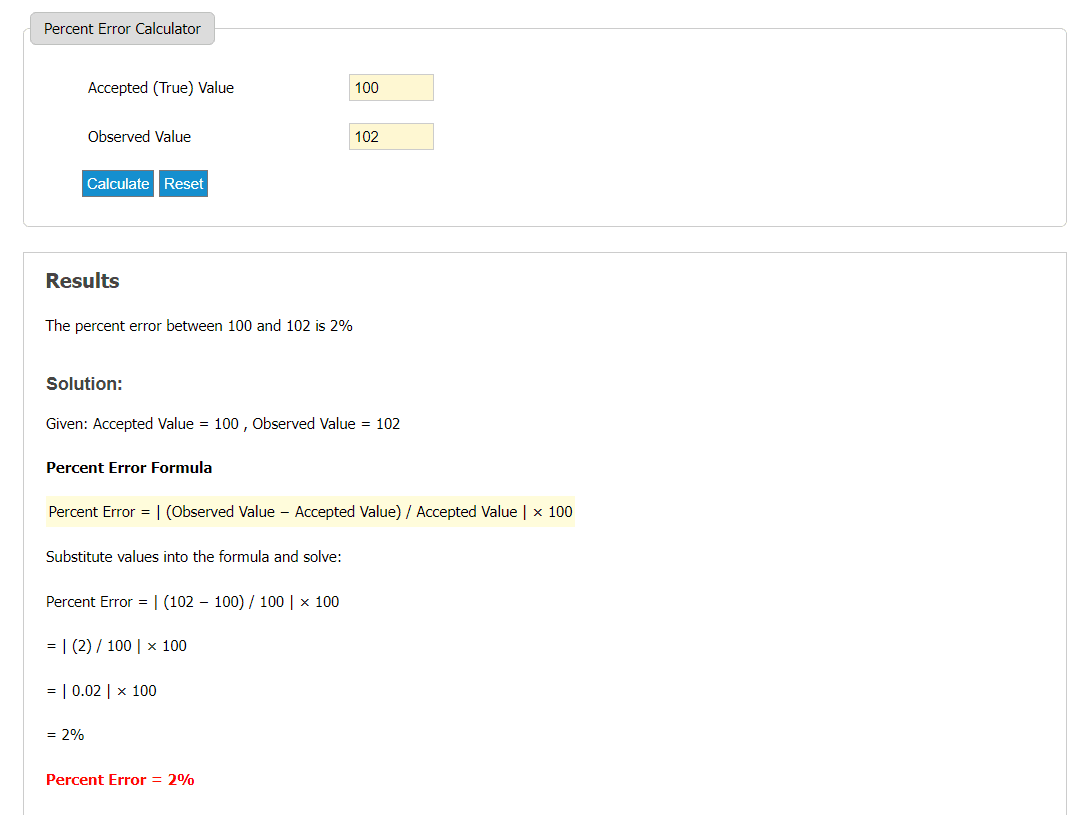
Kalkulačky jsou tedy ideální pro výpočet procentuální odchylky, pokud máte k dispozici rozsáhlá data a málo času.
Závěr
Chyby ve výpočtech mohou zkazit jakýkoli projekt nebo výzkum. Zde můžete využít online kalkulačky procentuálních odchylek, abyste práci provedli efektivněji a bez lidských chyb.
Pokud se zabýváte financemi, můžete si prohlédnout některé z těchto kalkulaček ziskového rozpětí.