V tomto návodu se ponoříme do tajů násobení dvou matic v Pythonu. Probereme si, jak ověřit podmínky pro platné násobení a sami si napíšeme funkci pro tento výpočet. Ukážeme si také alternativu s využitím vnořených seznamů. Nakonec se podíváme, jak k efektivnímu násobení matic využít knihovnu NumPy a její vestavěné funkce.
Jak ověřit, zda je násobení matic možné
Než se vrhneme na kód, připomeňme si základní pravidlo pro násobení matic. Násobení matice A maticí B je platné pouze tehdy, pokud počet sloupců matice A odpovídá počtu řádků matice B. Možná už jste se s tímto pravidlem setkali, ale zamysleli jste se někdy, proč tomu tak je?
Důvod tkví v samotné definici násobení matic. V obecném případě má matice A rozměry m x n (m řádků a n sloupců) a matice B má rozměry n x p (n řádků a p sloupců).
Jaké rozměry má výsledná matice?
Prvek na pozici (i, j) ve výsledné matici C se získá jako skalární součin i-tého řádku matice A a j-tého sloupce matice B.
Pro získání prvku na konkrétní pozici ve výsledné matici C tedy musíme spočítat skalární součin odpovídajícího řádku a sloupce z matic A a B. Opakováním tohoto postupu získáme matici C o rozměrech m x p (m řádků a p sloupců), jak je znázorněno níže.
Skalární součin (nebo také vnitřní součin) dvou vektorů a a b se vypočítá dle vzorce:

Shrňme si to:
- Skalární součin je definován pouze mezi vektory se stejným počtem prvků.
- Pro platné provedení skalárního součinu mezi řádkem a sloupcem při násobení matic musí mít oba vektory stejný počet prvků.
- V našem příkladu má každý řádek matice A n prvků a každý sloupec matice B má také n prvků.
Číslo n je zároveň počtem sloupců v matici A a počtem řádků v matici B. A proto se musí počet sloupců matice A rovnat počtu řádků matice B.
Doufám, že nyní lépe rozumíte podmínce platnosti násobení matic a tomu, jak se vypočítává každý prvek výsledné matice.
Pojďme si to vyzkoušet s kódem v Pythonu.
Vytvoření vlastní funkce pro násobení matic
Nejprve si vytvoříme vlastní funkci pro násobení matic. Tato funkce:
- Přijme dvě matice A a B jako vstupní parametry.
- Ověří, zda je násobení matic A a B platné.
- Pokud je násobení platné, vynásobí matice A a B a vrátí výslednou matici C.
- V opačném případě vrátí chybovou hlášku, že matice A a B nelze vynásobit.
Krok 1: Vygenerujeme dvě matice celých čísel pomocí funkce random.randint() z knihovny NumPy. Matice lze také vytvořit jako vnořené seznamy v Pythonu.
import numpy as np
np.random.seed(27)
A = np.random.randint(1,10,size = (3,3))
B = np.random.randint(1,10,size = (3,2))
print(f"Matice A:n {A}n")
print(f"Matice B:n {B}n")
# Výstup
Matice A:
[[4 9 9]
[9 1 6]
[9 2 3]]
Matice B:
[[2 2]
[5 7]
[4 4]]
Krok 2: Nyní definujeme funkci multiply_matrix(A,B), která přijímá matice A a B a vrací výslednou matici C, pokud je násobení platné.
def multiply_matrix(A,B):
global C
if A.shape[1] == B.shape[0]:
C = np.zeros((A.shape[0],B.shape[1]),dtype = int)
for row in range(rows):
for col in range(cols):
for elt in range(len(B)):
C[row, col] += A[row, elt] * B[elt, col]
return C
else:
return "Omlouvám se, matice A a B nelze vynásobit."
Analýza definice funkce
Pojďme si rozebrat definici funkce krok za krokem.
Deklarace C jako globální proměnné: V Pythonu mají proměnné definované uvnitř funkce lokální obor platnosti. Nelze k nim tedy přistupovat zvenčí funkce. Abychom měli k výsledné matici C přístup i mimo funkci, musíme ji deklarovat jako globální proměnnou. To provedeme pomocí klíčového slova global před názvem proměnné.
Ověření platnosti násobení matic: K ověření, zda lze matice A a B násobit, použijeme atribut shape. Pro libovolné pole arr, arr.shape[0] a arr.shape[1] nám dají počet řádků a sloupců. Podmínka A.shape[1] == B.shape[0] tedy ověří platnost násobení. Pouze pokud je tato podmínka pravdivá, vypočítá se výsledná matice. V opačném případě funkce vrátí chybové hlášení.
Vnořené cykly pro výpočet hodnot: K výpočtu prvků výsledné matice potřebujeme iterovat přes řádky matice A (vnější cyklus for). Vnitřní cyklus for nám umožňuje procházet sloupce matice B. Nejvnitřnější cyklus for umožňuje přístup ke každému prvku ve vybraném sloupci.
▶️ Nyní, když víme, jak naše funkce pro násobení matic funguje, můžeme ji zavolat s maticemi A a B, které jsme si dříve vygenerovali.
multiply_matrix(A,B)
# Výstup
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
Protože je násobení matic A a B platné, funkce multiply_matrix() vrací výslednou matici C.
Násobení matic pomocí vnořeného seznamu v Pythonu
V předchozí části jsme si vytvořili vlastní funkci pro násobení matic. Nyní si ukážeme, jak k dosažení stejného výsledku můžeme využít vnořené seznamy.
Zde je vnořený seznam pro násobení matic:
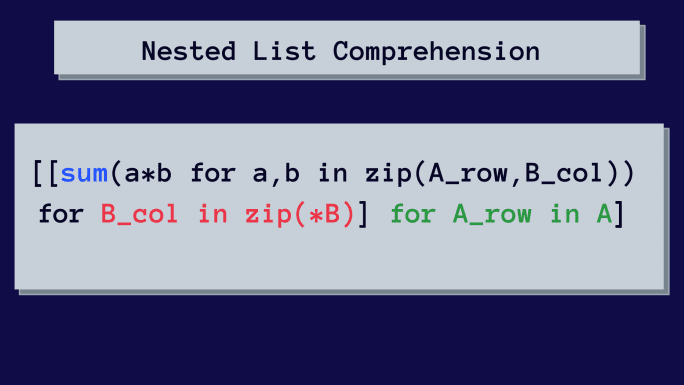
Na první pohled to může vypadat složitě, ale rozebereme si vnořený seznam krok za krokem.
Zaměříme se na jednotlivé seznamy a ukážeme si, co dělají.
Pro pochopení seznamů budeme používat obecnou šablonu:
[<do-this> for <item> in <iterable>]
kde,
<do-this>: co chcete udělat – výraz nebo operace
<item>: každý prvek, na který chcete operaci provést
<iterable>: iterovatelný objekt (seznam, tuple atd.), kterým procházíte
▶️ Pokud se chcete dozvědět více o seznamech v Pythonu, podívejte se na náš návod Seznam porozumění v Pythonu – s příklady.
Než budeme pokračovat, uvědomme si, že naším cílem je vytvořit výslednou matici C postupně po řádcích.
Vysvětlení vnořeného seznamu
Krok 1: Výpočet jedné hodnoty v matici C
Pro daný řádek i matice A a sloupec j matice B, nám níže uvedený výraz dá prvek na pozici (i, j) v matici C.
sum(a*b for a,b in zip(A_row, B_col)
# zip(A_row, B_col) vrací iterátor tuplů
# Pokud A_row = [a1, a2, a3] & B_col = [b1, b2, b3]
# zip(A_row, B_col) vrátí (a1, b1), (a2, b2) atd.
Pokud i = j = 1, výraz vrátí prvek c_11 matice C. Tímto způsobem získáme jeden prvek v jednom řádku.
Krok 2: Vytvoření jednoho řádku matice C
Naším dalším cílem je sestavit celý řádek.
Pro řádek 1 v matici A musíte projít všechny sloupce v matici B, abyste získali celý jeden řádek v matici C.
Vraťme se k naší šabloně seznamu:
- Nahraďte <do-this> výrazem z kroku 1.
- Nahraďte <item> za B_col – každý sloupec v matici B.
- Nakonec nahraďte <iterable> za zip(*B) – seznam obsahující všechny sloupce v matici B.
Zde je první část vnořeného seznamu.
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * je operátor pro "rozbalení" # zip(*B) vrací seznam sloupců v matici B
Krok 3: Sestavení všech řádků a získání matice C
Dále musíme doplnit zbytek matice C výpočtem dalších řádků.
K tomu musíme projít všechny řádky v matici A.
Vraťme se zpět k šabloně seznamu a proveďme následující:
- Nahraďte <do-this> seznamem z kroku 2. Připomeňme, že jsme v předchozím kroku vypočítali celý řádek.
- Nahraďte <item> za A_row – každý řádek v matici A.
- A vaše <iterovatelná> je samotná matice A při procházení jejích řádků.
A tady je konečná podoba našeho vnořeného seznamu.🎊
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A]
Je čas ověřit výsledek! ✔
# Přetypujeme na NumPy pole pomocí np.array()
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A])
# Výstup:
[[ 89 107]
[ 47 49]
[ 40 44]]
Pokud se na to podíváte blíže, je to ekvivalent vnořených cyklů for, které jsme měli předtím – jen stručnější.
Můžete to udělat ještě efektivněji pomocí některých vestavěných funkcí. Pojďme se o nich dozvědět v další části.
Násobení matic pomocí NumPy matmul()
Funkce np.matmul() přijímá dvě matice jako vstup a vrací jejich součin, pokud je násobení platné.
C = np.matmul(A,B)
print(C)
# Výstup:
[[ 89 107]
[ 47 49]
[ 40 44]]
Všimněte si, jak je tato metoda jednodušší než dvě předchozí. Místo np.matmul() můžeme také použít operátor @. Ukážeme si to hned.
Násobení matic pomocí operátoru @ v Pythonu
V Pythonu se operátor @ používá pro násobení matic.
Pracuje se dvěma maticemi (nebo obecněji s N-rozměrnými poli NumPy) a vrací jejich součin.
Poznámka: K používání operátoru @ potřebujete Python 3.5 nebo novější.
Zde je ukázka jeho použití.
C = A @ B
print(C)
# Výstup
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
Výsledná matice C je stejná jako v předchozích příkladech.
Lze použít np.dot() pro násobení matic?
Pokud jste někdy viděli kód, který používá np.dot() k násobení dvou matic, funguje to následovně:
C = np.dot(A,B)
print(C)
# Výstup:
[[ 89 107]
[ 47 49]
[ 40 44]]
Vidíte, že i np.dot(A, B) vrátí očekávanou matici součinu.
Nicméně, jak je uvedeno v dokumentaci NumPy, měli byste np.dot() používat pouze pro výpočet skalárního součinu dvou jednorozměrných vektorů a ne pro násobení matic.
Připomeňme, že prvek na pozici (i, j) matice C je skalární součin i-tého řádku matice A a j-tého sloupce matice B.
Protože NumPy implicitně provádí tento skalární součin pro všechny řádky a všechny sloupce, získáte výslednou matici součinu. Aby byl ale váš kód čitelný a předešlo se nejasnostem, používejte místo toho np.matmul() nebo operátor @.
Závěr
🎯 V tomto návodu jsme si probrali následující:
- Podmínku platnosti násobení matic: počet sloupců v matici A = počet řádků v matici B.
- Jak napsat vlastní funkci v Pythonu, která ověří platnost násobení matic a vrátí výslednou matici. Tělo funkce používá vnořené cykly for.
- Jak používat vnořené seznamy pro násobení matic. Jsou stručnější než cykly for, ale hůře se čtou.
- Jak používat vestavěnou funkci NumPy
np.matmul()pro násobení matic a že je to z hlediska rychlosti nejefektivnější metoda. - Seznámili jsme se s operátorem
@pro násobení matic v Pythonu.
Tím končí naše diskuse o násobení matic v Pythonu. Podívejte se na naše další návody, například Jak ověřit, zda je číslo prvočíslo v Pythonu, nebo řešení problémů s textovými řetězci v Pythonu.
Příjemné učení! 🎉