Jak vytisknout Pascalův trojúhelník v Pythonu

Tento tutoriál vás naučí, jak vytisknout Pascalův trojúhelník v Pythonu pro daný počet řádků.

Začnete tím, že se naučíte sestrojit Pascalův trojúhelník. Poté budete pokračovat v psaní funkce Pythonu a naučíte se ji dále optimalizovat.

▶️ Začínáme!

Table of Contents

Co je Pascalův trojúhelník a jak jej sestrojit?

Tisk Pascalova trojúhelníku pro daný počet řádků je oblíbená otázka při pohovoru.

V Pascalově trojúhelníku s n řádky má řádek číslo i i prvků.

První řádek má tedy jeden prvek, a to 1. A každý prvek v následujících řádcích je součtem dvou čísel přímo nad ním.

Následující obrázek vysvětluje, jak sestrojit Pascalův trojúhelník s pěti řadami.

Pascalův trojúhelník pro numRows = 5 (Obrázek od autora)

Všimněte si, jak můžete doplnit nuly, když máte pouze jedno číslo nad určitým číslem.

📝Jako rychlé cvičení postupujte podle výše uvedeného postupu a sestavte Pascalův trojúhelník pro n = 6 a n = 7.

Dále pojďme napsat nějaký kód. Můžete se rozhodnout spouštět úryvky kódu na Wdzwdz’s Python IDE přímo z vašeho prohlížeče – při procházení výukovým programem.

Funkce Pythonu pro tisk Pascalova trojúhelníku

V této sekci napíšeme funkci Pythonu pro tisk Pascalova trojúhelníku pro libovolný počet řádků.

Je třeba zvážit dvě klíčové otázky:

Jak vyjádřit položky v Pascalově trojúhelníku?
Jak vytisknout Pascalův trojúhelník s vhodnými mezerami a formátováním?

Pojďme si na ně nyní odpovědět.

#1. Jaký je výraz pro každou položku v Pascalově trojúhelníku?

Tak se stane, že záznamy v Pascalově trojúhelníku lze získat pomocí vzorce pro nCr. Pokud si pamatujete ze školní matematiky, nCr označuje počet způsobů, jak si můžete vybrat r položek ze sady n položek.

Vzorec pro nCr je uveden níže:

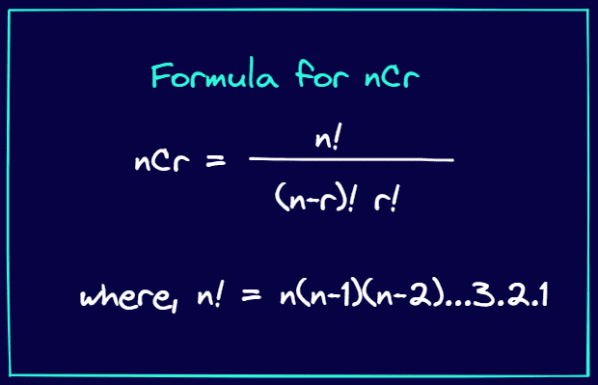Vzorec nCr (Obrázek od autora)

Nyní přistoupíme k vyjádření položek v Pascalově trojúhelníku pomocí vzorce nCr.

Pascalovy trojúhelníky pomocí nCr (obrázek autor)

Nyní jsme našli způsob, jak vyjádřit položky v matici.

#2. Jak upravit mezery při tisku vzoru?

V Pascalově trojúhelníku s numRows má řádek č. 1 jednu položku, řádek č. 2 má dvě položky a tak dále. Chcete-li vzor vytisknout jako trojúhelník, budete potřebovat numRows – i mezery v řádku #i. A k tomu můžete použít funkci rozsahu Pythonu ve spojení se smyčkou for.

Má Xbox Mario Kart?

Protože funkce range ve výchozím nastavení vylučuje koncový bod, nezapomeňte přidat + 1, abyste získali požadovaný počet úvodních mezer.

Nyní, když jste se naučili reprezentovat položky a také upravovat prostor při tisku Pascalova trojúhelníku, pojďme do toho a definujte funkci pascal_tri.

Analýza definice funkce

Co tedy chcete, aby funkce pascal_tri dělala?

Funkce pascal_tri by měla jako argument přijmout počet řádků (numRows).
Měl by vytisknout Pascalův trojúhelník s numRows.

Abychom vypočítali faktoriál, použijme funkci faktoriálu z vestavěného matematického modulu Pythonu.

▶️ Spusťte následující buňku kódu pro import faktoriálu a jeho použití ve vašem aktuálním modulu.

from math import factorial

Níže uvedený fragment kódu obsahuje definici funkce.

def pascal_tri(numRows):
  '''Print Pascal's triangle with numRows.'''
  for i in range(numRows):
    # loop to get leading spaces
	  for j in range(numRows-i+1):
		  print(end=" ")
    
    # loop to get elements of row i
	  for j in range(i+1):
		  # nCr = n!/((n-r)!*r!)
		  print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")

	 # print each row in a new line
	  print("n")

Funkce funguje následovně:

Funkce pascal_tri má jeden povinný parametr numRows: počet řádků.
Celkem je řádků numRows. Pro každý řádek i přidáme numRows – i úvodní mezery před první záznam v řádku.
K výpočtu jednotlivých položek pak použijeme vzorec nCr. Pro řádek i jsou položky iCj, kde j = {0,1,2,..,i}.
Všimněte si, že používáme //, který provádí celočíselné dělení, protože bychom chtěli, aby položky byly celá čísla.
Po vypočítání všech položek v řadě vytiskněte další řádek na nový řádek.

🔗 Jak jsme přidali a dokumentační řetězec, můžete použít vestavěnou funkci nápovědy Pythonu nebo atribut __doc__ pro přístup k dokumentačnímu řetězci funkce. Níže uvedený fragment kódu ukazuje, jak na to.

help(pascal_tri)

# Output
Help on function pascal_tri in module __main__:

pascal_tri(numRows)
    Print Pascal's triangle with numRows.

pascal_tri.__doc__

# Output
Print Pascal's triangle with numRows.

Nyní pojďme do toho a zavolejte funkci s počtem řádků jako argumentem.

pascal_tri(3)

# Output
     1
    1 1
   1 2 1

První 3 řádky Pascalova trojúhelníku jsou vytištěny podle očekávání.

Jak používat svůj Google Home Hub jako digitální fotorámeček

Vytiskněte Pascalův trojúhelník pomocí rekurze

V předchozí části jsme identifikovali matematické vyjádření každého záznamu v Pascalově trojúhelníku. Nepoužili jsme však vztah mezi položkami ve dvou po sobě jdoucích řádcích.

Ve skutečnosti jsme použili předchozí řádek k výpočtu položek v následujícím řádku. Nemůžeme toho využít a přijít s rekurzivní implementací funkce pascal_tri?

Ano, pojďme na to!

V rekurzivní implementaci funkce opakovaně volá sama sebe, dokud není splněn základní případ. Při konstrukci Pascalova trojúhelníku začínáme první řadou s jedním záznamem 1 a poté sestavujeme další řady.

Volání funkce pascal_tri(numRows) tedy volá pascal_tri(numRows-1) a tak dále, dokud není dosaženo základního případu pascal_tri(1).

Zvažte příklad, kdy potřebujete vytisknout první 3 řádky Pascalova trojúhelníku. Následující obrázek vysvětluje, jak jsou rekurzivní volání tlačena do zásobníku. A jak volání rekurzivní funkce vrací řádky Pascalova trojúhelníku.

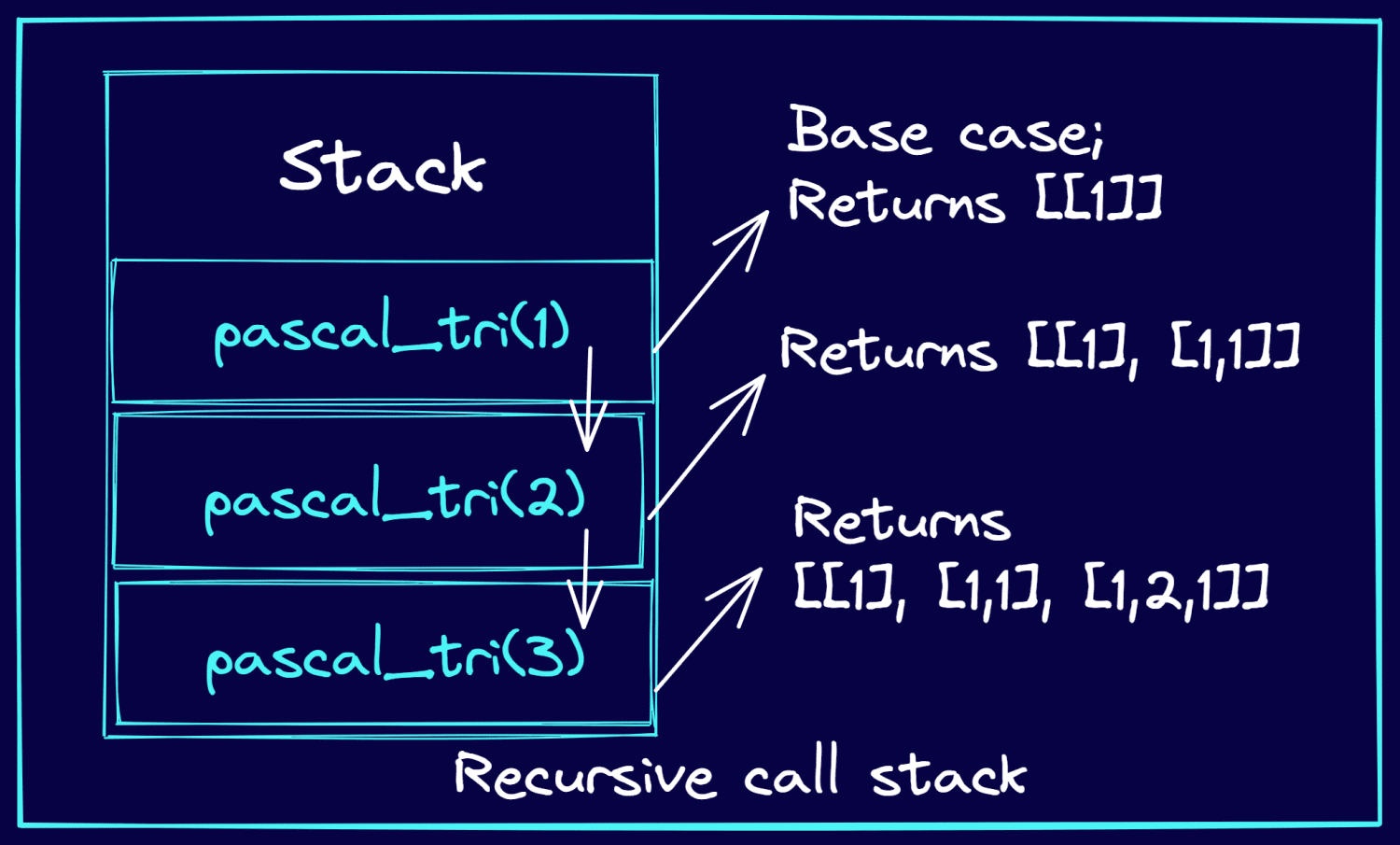Zásobník volání během rekurzivních volání (obrázek od autora)

▶️ Spusťte níže uvedený úryvek kódu a vygenerujte rekurzivně řádky Pascalova trojúhelníku.

def pascal_tri(numRows):
    '''Print Pascal's triangle with numRows.'''
    if numRows == 1:
        return [[1]] # base case is reached!
    else:
        res_arr = pascal_tri(numRows-1) # recursive call to pascal_tri
        # use previous row to calculate current row 
        cur_row = [1] # every row starts with 1
        prev_row = res_arr[-1] 
        for i in range(len(prev_row)-1):
            # sum of 2 entries directly above
            cur_row.append(prev_row[i] + prev_row[i+1]) 
        cur_row += [1] # every row ends with 1
        res_arr.append(cur_row)
        return res_arr

Zde je několik bodů, které stojí za zmínku:

Jako datovou strukturu jsme použili vnořený seznam, kde každý řádek v Pascalově trojúhelníku je seznam sám o sobě, jako je tento: [[row 1], [row 2],…,[row n]].
Volání funkce pascal_tri(numRows) spouští řadu rekurzivních volání s argumenty numRows – 1, numRows – 2 až po 1. Tato volání jsou přesunuta do zásobníku.
Když numRows == 1, dosáhli jsme základního případu a funkce se vrátí [[1]].
Nyní vrácený seznam používají následující funkce v zásobníku volání – k výpočtu dalšího řádku.
Pokud je aktuální řádek cur_row, pak cur_row[i] = předchozí_řádek[i] + předchozí_řádek[i+1]—součet 2 prvků přímo nad aktuálním indexem.

Protože vrácené pole je vnořený seznam (seznam seznamů), musíme upravit mezery a vytisknout položky, jak je znázorněno v buňce kódu níže.

tri_array = pascal_tri(5)

for i,row in enumerate(tri_array):
  for j in range(len(tri_array) - i + 1):
    print(end=" ") # leading spaces
  for j in row:
    print(j, end=" ") # print entries
  print("n")  # print new line

Výstup je správný, jak je vidět níže!

Funkce Pythonu pro tisk Pascalova trojúhelníku pro numRows ≤ 5

Obě metody, které jste se naučili, budou fungovat pro tisk Pascalova trojúhelníku pro libovolný počet řádků numRows.

20 Nejčastějších otázek a odpovědí v rozhovoru pro DevOps [2022]

Jsou však chvíle, kdy potřebujete vytisknout Pascalův trojúhelník pro menší počet řádků. A když je počet řádků, které potřebujete vytisknout, maximálně 5 – můžete použít přímou techniku.

Projděte si obrázek níže. A pozorujte, jak jsou mocniny 11 totožné se záznamy v Pascalově trojúhelníku. Všimněte si také, že to funguje pouze do 4. mocniny 11. To znamená, že 11 umocněná na mocniny {0, 1, 2, 3, 4} dává záznamy v řádcích 1 až 5 Pascalova trojúhelníku.

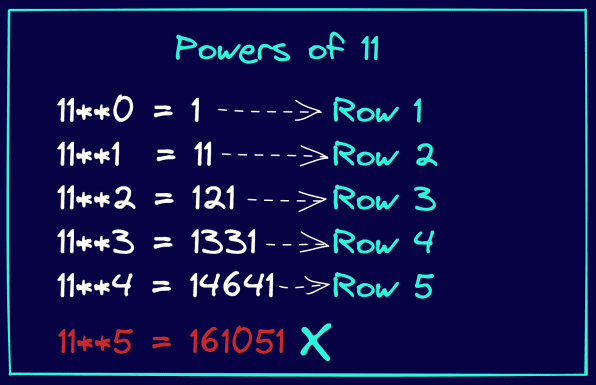
Pojďme přepsat definici funkce, jak je uvedeno níže:

def pascal_tri(numRows):
  '''Print Pascal's triangle with numRows.'''
  for i in range(numRows):
    print(' '*(numRows-i), end='')
    # compute power of 11
    print(' '.join(str(11**i)))

Takto funguje funkce pascal_tri:

Stejně jako u předchozích příkladů upravíme rozestup.
A pak použijeme Pythonův operátor umocňování (**) k výpočtu mocnin 11.
Protože mocniny 11 jsou ve výchozím nastavení celá čísla, převeďte je na řetězec pomocí str(). Nyní máte mocniny 11 jako struny.
Řetězce v Pythonu jsou iterovatelné, takže je můžete procházet a přistupovat k jednomu znaku po druhém.
Dále můžete použít metodu join() se syntaxí: .join() ke spojení prvků v pomocí jako oddělovače.
Zde potřebujete jednu mezeru mezi znaky, takže bude ‚ ‚, je řetězec: mocnina 11.

Pojďme zkontrolovat, zda funkce funguje tak, jak má.

pascal_tri(5)

# Output
     1
    1 1
   1 2 1
  1 3 3 1
 1 4 6 4 1

Jako další příklad zavolejte funkci pascal_tri s argumentem 4.

pascal_tri(4)

# Output
     1
    1 1
   1 2 1
  1 3 3 1

Doufám, že víte, jak můžete snadno vytisknout Pascalův trojúhelník pro numRows v rozsahu 1 až 5.

Závěr

Zde je to, co jsme se naučili:

Jak sestrojit Pascalův trojúhelník s daným počtem řádků. Každé číslo v každém řádku je součtem dvou čísel přímo nad ním.
Napište funkci Pythonu pomocí vzorce nCr = n!/(nr)!.r! vypočítat vstupy Pascalova trojúhelníku.
Poté jste se naučili rekurzivní implementaci funkce.
Nakonec jste se naučili nejoptimálnější metodu konstrukce Pascalova trojúhelníku pro počet řádků do 5 – s použitím mocnin 11.

Pokud chcete zlepšit dovednosti Pythonu, naučte se násobit matice, zkontrolujte, zda je číslo prvočíslo, a řešte problémy s operacemi s řetězci. Šťastné kódování!