Tento návod vás provede použitím funkce linspace() z knihovny NumPy v Pythonu pro generování posloupností čísel s rovnoměrnými rozestupy.
Probereme si syntaxi funkce linspace() a předvedeme praktické příklady, které vám pomohou pochopit její využití.
Poznámka: Před zahájením tohoto tutoriálu se ujistěte, že máte nainstalovaný Python a knihovnu NumPy.
Ještě nemáte NumPy? Připravili jsme pro vás stručný návod k instalaci.
Pojďme na to!
Instalace a import knihovny NumPy
Než začneme s praktickými ukázkami, podívejme se rychle na kroky potřebné k instalaci knihovny NumPy.
⏩ Pokud již máte NumPy nainstalovaný, můžete tento krok přeskočit.
- Pokud pracujete v prostředí Google Colab (cloudové prostředí Jupyter notebooku), můžete importovat NumPy a rovnou začít s kódováním. (Doporučeno pro tento tutoriál ✅)
- Pro lokální vývojové prostředí doporučujeme instalaci distribuce Anaconda Python. Anaconda obsahuje několik užitečných balíčků předinstalovaných. Stáhněte si instalační program pro váš operační systém. Nastavení je otázkou několika minut. ⌛
- I když již máte Python na svém počítači, můžete nainstalovat distribuci Anaconda. K instalaci a správě balíčků lze použít conda nebo pip. Pro instalaci NumPy použijte jeden z následujících příkazů v příkazovém řádku Anaconda.
# Instalace NumPy pomocí conda
conda install numpy
# Instalace NumPy pomocí pip
pip install numpy
V dalším kroku importujte knihovnu numpy s aliasem np pomocí následujícího příkazu. Díky tomu se můžete na NumPy odkazovat jako np, aniž byste museli pokaždé psát celé numpy.
import numpy as np
Dále budeme pro přístup k funkcím knihovny NumPy používat tečkovou notaci, například np.funkce.
Proč generovat čísla s rovnoměrnými rozestupy?
Při práci s poli NumPy se často setkáte se situací, kdy potřebujete vytvořit pole čísel, která jsou v daném intervalu rozložena rovnoměrně.
Než budeme pokračovat, rychle si porovnáme funkci np.linspace() s podobnou funkcí np.arange().
NumPy linspace() vs. NumPy arange()
Pokud jste již NumPy používali, pravděpodobně jste k vytvoření pole čísel v určitém rozsahu použili funkci np.arange().
Funkce np.arange(start, stop, step) vrací pole čísel od start do stop (vyloučeně), s krokem o velikosti step; výchozí velikost kroku je 1.
Hodnota kroku však nemusí být vždy zřejmá. Podívejme se na příklad:
Pokud například potřebujete 4 čísla rovnoměrně rozmístěná mezi 0 a 1, víte, že velikost kroku musí být 0,25. Pokud ale použijete np.arange(), neobsahuje koncovou hodnotu 1. Budete proto muset zadat interval, který přesahuje koncovou hodnotu.
Následující obrázek ilustruje několik příkladů, kdy potřebujete specifický počet rovnoměrně rozložených bodů v intervalu [a, b].
Rovnoměrně rozložené body v intervalu
Náš první příklad 4 rovnoměrně rozložených bodů [0,1] byl poměrně snadný. Velikost kroku mezi body by měla být 0,25.
Předpokládejme, že máte trochu složitější příklad – potřebujete 7 rovnoměrně rozložených bodů mezi 1 a 33. Zde nemusí být velikost kroku tak jasná. V tomto případě si ale můžete hodnotu kroku vypočítat ručně.
Nicméně, np.linspace() je tu od toho, aby vám to usnadnil! 😄
Použití NumPy linspace
Při použití np.linspace() stačí zadat počet bodů v intervalu – bez ohledu na velikost kroku. A získáte pole, které přesně potřebujete.
S touto motivací se v další části podívejme na syntaxi np.linspace().
Syntaxe NumPy linspace()
Syntaxe pro použití funkce linspace() z knihovny NumPy je následující:
np.linspace(start, stop, num, endpoint, retstep, dtype, axis)
Na první pohled se tato syntaxe s mnoha parametry může zdát komplikovaná.
Většina z nich je však volitelná a za chvíli se dostaneme k jednodušší syntaxi.
Nyní se podívejme na jednotlivé části syntaxe:
startastopjsou počáteční a koncové body intervalu. Mohou to být skalární hodnoty nebo pole. V tomto tutoriálu se omezíme na skalární počáteční a koncové hodnoty.numje počet rovnoměrně rozložených bodů. Tento parametr je volitelný s výchozí hodnotou 50.endpointje další volitelný parametr, který může mít hodnotuTrueneboFalse.- Výchozí hodnota je
True, což znamená, že koncový bod bude ve výchozím nastavení součástí intervalu. Můžete ho ale nastavit naFalse, pokud koncový bod nechcete zahrnout. retstepje další volitelný parametr, který přebírá booleovskou hodnotuTrueneboFalse. Pokud je nastaven naTrue, vrací se velikost kroku.dtypeje datový typ čísel v poli. Obvykle se datový typ odvodí jako floating-point a nemusí být explicitně zadán.axisje další volitelný parametr, který udává osu, podél které mají být čísla uložena. Je relevantní pouze v případě, že počáteční a koncové hodnoty jsou samy o sobě pole.
▶️ Co tedy funkce np.linspace() vrací?
Vrací N-rozměrné pole rovnoměrně rozložených čísel. Pokud je parametr retstep nastaven na True, vrací také velikost kroku.
Na základě naší dosavadní diskuse zde je zjednodušená syntaxe pro použití funkce np.linspace():
np.linspace(start, stop, num)
Výše uvedený kód vrátí pole s num rovnoměrně rozloženými čísly v intervalu [start, stop].
Nyní, když znáte syntaxi, začněme s praktickými příklady kódování.
Jak vytvářet pole s rovnoměrnými rozestupy pomocí NumPy linspace()
#1. Jako první příklad vytvoříme pole s 20 rovnoměrně rozloženými čísly v intervalu [1, 5].
Hodnoty pro start, stop a num můžete zadat jako klíčové argumenty. To je ukázáno v následující buňce s kódem:
import numpy as np
arr1 = np.linspace(start = 1,stop = 5,num = 20)
print(arr1)
# Výstup:
# [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
# 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
# 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
# 4.78947368 5. ]
Všimněte si, jak čísla v poli začínají na 1 a končí na 5, včetně obou koncových bodů. Také si všimněte, že čísla včetně 1 a 5 jsou v poli reprezentována jako floating-point čísla.
#2. V předchozím příkladu jste hodnoty pro start, stop a num zadali jako klíčové argumenty. Pokud argumenty zadáte ve správném pořadí, můžete je použít také jako poziční argumenty, pouze s hodnotami, jak je uvedeno níže.
import numpy as np
arr2 = np.linspace(1,5,20)
print(arr2)
# Výstup:
# [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
# 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
# 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
# 4.78947368 5. ]
#3. Nyní vytvoříme další pole, kde nastavíme parametr retstep na True.
To znamená, že funkce nyní vrátí pole a také krok. Můžeme je rozbalit do dvou proměnných: arr3 (pole) a step_size (velikost kroku).
Následující buňka s kódem ukazuje, jak to můžete udělat.
import numpy as np
arr3, step_size = np.linspace(1,5,20,retstep = True)
print(arr3)
# Výstup:
# [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
# 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
# 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
# 4.78947368 5. ]
# Výstup:
print(step_size)
# 0.21052631578947367
#4. Jako poslední příklad nastavíme parametr endpoint na False a zkontrolujeme, co se stane.
import numpy as np
arr4 = np.linspace(1,5,20,endpoint = False)
print(arr4)
# Výstup:
# [1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8
# 4. 4.2 4.4 4.6 4.8]
Ve vráceném poli vidíte, že 1 je zahrnuta, zatímco 5 není. Poslední hodnota v poli je 4,8, ale stále máme 20 čísel.
Zatím jsme generovali jen pole s rovnoměrnými rozestupy. V další části si vizualizujeme vygenerovaná čísla pomocí grafu.
Jak vykreslit rovnoměrně rozložená čísla v intervalu
V této části vybereme interval [10, 15]. Pomocí np.linspace() vygenerujeme dvě pole, jedno s 8 a druhé s 12 body.
Po vygenerování můžeme k vykreslení použít funkci z knihovny matplotlib.
Pro přehlednost umístíme dvě pole (N1 = 8 a N2 = 12) s rovnoměrně rozloženými body do různých pozic na ose y.
Následující kód to ukazuje.
import numpy as np
import matplotlib.pyplot as plt
N1 = 8
N2 = 12
a = 10
b = 15
y1 = np.zeros(N1)
y2 = np.zeros(N2)
x1 = np.linspace(a, b, N1)
x2 = np.linspace(a, b, N2)
plt.plot(x1, y1-0.5, 'o')
plt.plot(x2, y2 + 0.5, 'o')
plt.ylim([-1, 1])
plt.title(f'Rovnoměrně rozmístěná čísla v intervalu [{a},{b}]')
plt.xlabel('Interval')
plt.show()
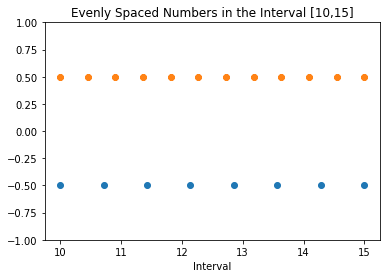
Generování rovnoměrně rozložených bodů je užitečné při práci s matematickými funkcemi. O tom se dozvíme v další části.
Jak používat NumPy linspace() s matematickými funkcemi
Po vygenerování pole s rovnoměrně rozloženými čísly pomocí funkce np.linspace() můžete vypočítat hodnoty matematických funkcí v daném intervalu.
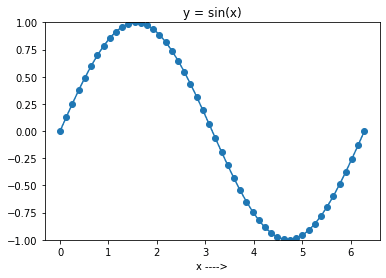
V níže uvedeném kódu nejprve vygenerujeme 50 rovnoměrně rozložených bodů v intervalu 0 až 2π. Potom vytvoříme pole y pomocí funkce np.sin() na poli x. Všimněte si, že parametr num můžeme přeskočit, protože výchozí hodnota je 50. I tak ho ale budeme používat explicitně.
V dalším kroku vykreslíme funkci sinus v intervalu [0, 2π]. K tomu můžeme použít matplotlib, stejně jako v předchozím příkladu. Konkrétně se funkce plot() v matplotlib.pyplot používá k vytvoření spojnicového grafu.
import numpy as np
import matplotlib.pyplot as plt
N = 50
a = 0.0
b = 2*np.pi
x = np.linspace(a, b, N)
y = np.sin(x)
plt.plot(x, y, marker = "o")
plt.ylim([-1, 1])
plt.title(f'y = sin(x)')
plt.xlabel('x ---->')
plt.show()
Nyní spusťte výše uvedený kód s nastavenou hodnotou N na 10. Získáte graf, jak je znázorněno na obrázku níže.
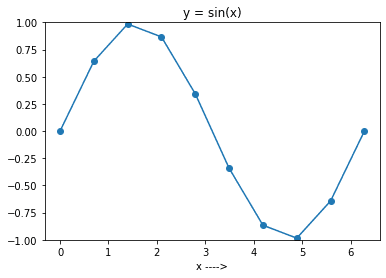
Můžete vidět, že graf není příliš hladký, protože jsme v intervalu vybrali pouze 10 bodů.
Obecně platí, že čím větší počet bodů berete v úvahu, tím hladší bude graf funkce.
Závěr
Zde je shrnutí toho, co jsme se naučili.
np.linspace(start, stop, num)vrací pole snumrovnoměrně rozloženými čísly v intervalu [start,stop].- Pokud chcete vyloučit koncový bod, nastavte volitelný parametr
endpointnaFalse, čímž se interval změní na [start,stop). - Volitelně můžete nastavit parametr
retstepnaTruepro získání velikosti kroku. - Generujte pole s rovnoměrnými rozestupy pomocí
np.linspace()a poté s nimi pracujte s matematickými funkcemi.
Doufám, že nyní rozumíte tomu, jak funkce np.linspace() funguje. Výše uvedené příklady si můžete sami spustit v Jupyter notebooku. Podívejte se na našeho průvodce Jupyter notebookem nebo na další alternativy Jupyter, které byste mohli zvážit.
Brzy se uvidíme v dalším tutoriálu o Pythonu. Do té doby pokračujte v kódování! 😀