Úprava datových seznamů je naprosto klíčová pro fungování aplikací.
Umožňuje efektivní prezentaci a vyhledávání informací. Proto je nezbytné, aby každý zkušený softwarový inženýr měl dokonalou znalost algoritmů pro třídění polí. V tomto textu si projdeme nejběžnější metody pro uspořádávání prvků v JavaScriptu.
Co je to třídění a proč je důležité?
Zdroj: Unsplash
Třídění představuje systematické seřazování hodnot podle předem stanovených kritérií. Toto uspořádání může probíhat vzestupně nebo sestupně. Úprava polí v JavaScriptu je přínosná, protože zjednodušuje interpretaci a zobrazení dat.
Například uživatelé mohou preferovat zobrazení souborů od nejnovějších nebo produktů seřazených dle ceny. Je také neocenitelné při binárním vyhledávání, které vyžaduje seřazené vstupy.
Přestože existují funkce a knihovny pro snadné třídění, je klíčové rozumět principům fungování algoritmů. Je to nezbytné pro kódovací pohovory a v situacích, kdy je potřeba pracovat s kódem na nízké úrovni.
Algoritmy pro třídění polí v JavaScriptu
Bublinové třídění

Bublinové třídění je považováno za jeden z nejjednodušších algoritmů k pochopení a implementaci. Jeho základem je iterace přes pole. Při každém průchodu se porovnávají sousední elementy a v případě, že jsou ve špatném pořadí, se prohodí.
Celkový počet průchodů se rovná počtu prvků v poli. Při každé iteraci se prvky postupně řadí od konce pole. Zde je pseudokód pro řazení čísel vzestupně:
1. Nechť n je počet prvků v poli 2. Opakuj n-krát, použij proměnnou i pro počítání průchodů (v každém cyklu proveď následující): a. Projdi pole od druhého elementu do (n - i)-tého elementu b. Pokud je předchozí element větší než aktuální, prohoď je.
Implementace v JavaScriptu vypadá takto:
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
Pro lepší pochopení doporučuji vložit do vnitřních smyček `console.log`, abyste mohli sledovat změny v poli během jednotlivých průchodů.
V následujícím příkladu je funkce upravena tak, aby zobrazovala mezikroky. Vytvoříme také malé neseřazené pole a použijeme na něj funkci pro třídění.
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
console.log(`Průchod: ${i}`);
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
console.log(arr);
}
}
return arr;
}
const array = [9, 2, 7, 4, 1];
sort(array);
console.log(array);
Výsledkem spuštění tohoto kódu bude:

Bublinové třídění má časovou složitost O(n^2), protože vyžaduje n průchodů a při každém z nich prochází polem. Proto není příliš efektivní pro velké datové soubory. Nicméně jeho prostorová složitost je O(1), protože upravuje prvky přímo v daném poli.
Třídění vkládáním

Třídění vkládáním je dalším oblíbeným algoritmem pro řazení polí v JavaScriptu. Funguje tak, že se postupně vybírá prvek (označme ho `num`) a posouvá se vlevo, dokud se nenarazí na menší hodnotu. Tento proces probíhá od druhého prvku pole do konce. Zde je pseudokód:
1. Nechť n je počet prvků v poli
2. Procházej pole od i = 1 do n - 1 (začni od druhého prvku)
a. Ulož hodnotu array[i] do currentElement
b. Nastav j = i - 1
c. Dokud je j >= 0 a array[j] > current_element
i. Přesuň array[j] na array[j+1]
ii. Sniž j o 1
d. Nastav array[j+1] na current_element
A nyní implementace pseudokódu v JavaScriptu:
function insertionSort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
}
return array;
}
Stejně jako u bublinového třídění, přidání `console.log` usnadní vizualizaci postupu. Následující kód demonstruje řazení vkládáním v akci:
function sort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
console.log("Vkládám element:", currentElement);
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
console.log("Vloženo na pozici:", j + 1);
console.log(array);
}
return array;
}
const array = [4, 1, 2, 5, 3];
sort(array);
Spuštění tohoto kódu povede k následujícímu výsledku:
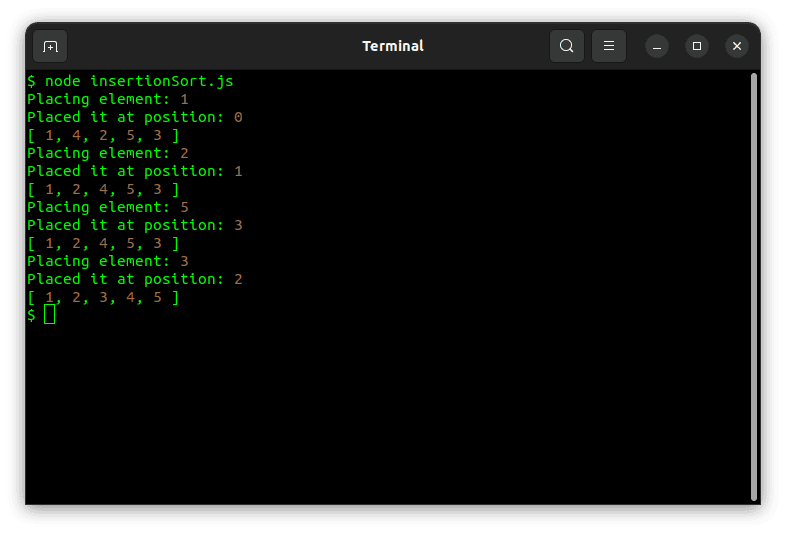
Třídění slučováním

Zatímco třídění vkládáním a bublinové třídění mají kvadratickou časovou složitost, třídění slučováním dosahuje kvazilineární složitosti O(n * log(n)).
Třídění slučováním je založeno na principu „rozděl a panuj“. Pole je opakovaně děleno na menší podpole, dokud nezůstanou pouze jednoprvková pole. Následně se tyto podpole zpětně slučují.
Dělení probíhá rekurzivně, což umožňuje následné opětovné složení pole.
Při slučování podpolí se tyto podpole skládají do seřazeného celku. Sloučení probíhá podobně jako sloučení dvou seřazených polí. Pseudokód je uveden níže:
1. Pokud je délka pole menší nebo rovna 1, vrať pole (základní případ)
2. Najdi prostřední index:
a. Nastav mid na dolní celou část (délka pole / 2)
3. Rozděl pole na dvě podpole:
a. Vytvoř leftArray a zkopíruj do něj první polovinu pole (od indexu 0 do mid)
b. Vytvoř rightArray a zkopíruj do něj druhou polovinu pole (od indexu mid+1 do konce)
4. Rekurzivně zavolej MergeSort na leftArray
5. Rekurzivně zavolej MergeSort na rightArray
6. Sloučí dvě seřazená podpole:
a. Vytvoř prázdné resultArray
b. Dokud nejsou leftArray a rightArray prázdné:
i. Pokud je první element v leftArray menší nebo roven prvnímu elementu v rightArray, připoj ho k resultArray
ii. Jinak připoj první element v rightArray k resultArray
c. Připoj všechny zbývající elementy z leftArray k resultArray (pokud existují)
d. Připoj všechny zbývající elementy z rightArray k resultArray (pokud existují)
7. Vrať resultArray
Jeho implementace v JavaScriptu by vypadala takto:
function sort(array) {
// Základní případ, kdy zastavíme dělení pole
if (array.length == 1) {
return array;
}
// Nalezení středu pole
const m = Math.round(array.length / 2);
// Rozdělení pole na dvě poloviny
const leftUnsorted = array.slice(0, m);
const rightUnsorted = array.slice(m);
// Rekurzivní volání funkce merge sort
const leftSorted = sort(leftUnsorted);
const rightSorted = sort(rightUnsorted);
// Vrácení seřazeného sloučeného pole
return merge(leftSorted, rightSorted);
}
function merge(left, right) {
// Sloučení dvou seřazených seznamů
let result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex += 1;
} else {
result.push(right[rightIndex]);
rightIndex += 1;
}
}
return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}
Pokud kód spustíte s testovacím polem, měl by správně fungovat.
Rychlé třídění

Stejně jako třídění slučováním, i rychlé třídění (Quick Sort) využívá strategii „rozděl a panuj“. Algoritmus vybere prvek pivotu. Poté přesune všechny prvky větší než pivot doprava a menší než pivot doleva. Po dokončení bude pivot na správné pozici.
Pro přesun prvků se pivot nejprve přesune na konec pole.
Po přesunutí se zleva pole použije ukazatel pro hledání prvního čísla většího než pivot. Současně se zprava pole použije ukazatel pro hledání prvního čísla menšího než pivot. Jakmile se obě čísla najdou, prohodí se. Tento postup se opakuje, dokud ukazatel zleva nepřekročí ukazatel zprava.
V momentě zastavení se větší z naposled prohozených čísel prohodí s pivotem. Tím se pivot dostane na svou správnou pozici. Čísla menší než pivot budou vlevo a čísla větší vpravo.
Tento postup se rekurzivně opakuje pro podpole nalevo a napravo od pivotu, dokud nezůstane jen jedno číslo v každém podpoli.
Zde je pseudokód pro rychlé třídění:
1. Pokud je lessThanPointer menší než greaterThanPointer:
a. Vyber prvek pivotu z pole
b. Přesuň elementy tak, aby prvky menší byly vlevo a větší vpravo:
c. Rekurzivně zavolej Quicksort na leftSubarray
d. Rekurzivně zavolej Quicksort na rightSubarray
A implementace v JavaScriptu:
function sort(array, low, high) {
if (low < high) {
// Výběr indexu pivotu a rozdělení pole
const pivotIndex = move(array, low, high);
// Rekurzivní třídění podpolí vlevo a vpravo od pivotu
sort(array, low, pivotIndex - 1);
sort(array, pivotIndex + 1, high);
}
}
function move(array, low, high) {
// Vyber prvek pivotu (v tomto případě poslední element)
const pivotElement = array[high];
// Inicializace indexu pro menší element
let i = low - 1;
for (let j = low; j < high; j++) {
// Pokud je aktuální element menší nebo roven pivotu, prohoď ho s elementem na indexu i+1
if (array[j] <= pivotElement) {
i += 1;
const temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// Prohoď pivot element do správné pozice
const temp = array[i];
array[i] = array[j];
array[j] = temp;
// Vrať index pivot elementu
return i + 1;
}
Seřazení testovacího pole pomocí Quick Sort v Node.js by mělo vypadat následovně:
V nejlepším případě má rychlé třídění kvazilineární časovou složitost. Prostorová náročnost rychlého třídění se také mění logaritmicky. Proto je relativně efektivní v porovnání s jinými algoritmy pro třídění polí v JavaScriptu.
Tipy pro kódovací pohovory
❇️ Praxe je klíčová. Pomáhá pochopit různé algoritmy a především rozvíjet dovednosti v řešení problémů a logického myšlení. Můžete trénovat na platformách jako Leetcode a AlgoExpert.
❇️ Nejdříve se pokuste problém vyřešit sami. Snažte se vymyslet řešení, než se podíváte na hotové, protože vám to pomůže rozvinout schopnosti řešit problémy.
❇️ Pokud si s problémem nevíte dlouho rady, podívejte se na řešení. I z něj se můžete naučit, jak problém vyřešit. Většina výukových platforem poskytuje řešení. Pro pochopení konceptů můžete také využít ChatGPT nebo Google Bard.
❇️ Nepište kód hned. Prezentujte své řešení a promyslete ho před samotným psaním. Pseudokód je také užitečný pro rychlé zaznamenání nápadů.
Závěr
V tomto článku jsme si prošli nejčastěji používané algoritmy pro třídění. Osvojení si všech může zpočátku působit náročně. Proto se doporučuje kombinovat různé zdroje a nespoléhat se jen na jeden. Přeji hodně úspěchů při kódování!
Dále se můžete podívat na pochopení funkce třídění v Pythonu.