Zavedení procesu vyhledávání může být složité, ale rozhodně ne nemožné.
V běžném životě se při hledání neřídíme žádnými specifickými šablonami. Jednoduše se vydáme na místa, která považujeme za pravděpodobná. Většinou se obejdeme bez jakéhokoli pevného schématu.
Je tento přístup použitelný i ve světě programování?
Odpověď zní ne! V programování je nezbytné definovat určitý model pro vyhledávání informací. V tomto textu se podíváme na některé algoritmy, které při hledání využívají různé struktury.
Ve světě programování existuje mnoho vyhledávacích algoritmů. Zaměříme se na ty nejdůležitější a nejběžněji používané. Ostatní algoritmy pak snadno pochopíte sami.
Pro účely tohoto článku budeme vyhledáváním rozumět hledání konkrétního prvku v poli.
Pojďme se na jednotlivé algoritmy podívat podrobněji.
Lineární vyhledávání
Jak už název napovídá, lineární vyhledávací algoritmus postupuje při hledání prvků v poli lineárně. Začíná na začátku pole a postupně prochází všechny prvky až do konce, dokud nenajde hledaný prvek. Jakmile je prvek nalezen, program se zastaví.
Pro lepší pochopení si lineární vyhledávání ilustrujme na několika příkladech.
Pokud budeme pečlivě sledovat způsob vyhledávání, zjistíme, že čas potřebný k provedení programu je v nejhorším případě O(n). Při analýze algoritmů musíme zohledňovat právě nejhorší možnou časovou složitost. Časová složitost lineárního vyhledávání je tedy O(n).
Podívejme se, jak se lineární vyhledávání implementuje.
Implementace lineárního vyhledávání
Nyní, když máte základní znalost lineárního vyhledávání, je čas vyzkoušet si ho na praktickém příkladu. Nejprve si představíme kroky potřebné k implementaci algoritmu, a pak se pokusíme ho naprogramovat. Pokud by se vám to hned nepodařilo, nezoufejte, kód vám poskytnu následně.
Zde jsou kroky potřebné pro implementaci lineárního vyhledávání:
- Inicializujte pole s prvky (například s vašimi oblíbenými čísly).
- Napište funkci nazvanou `search_element`, která přijímá tři argumenty: pole, jeho délku a prvek, který hledáme.
- Funkce `search_element(arr, n, element)`:
- Projděte pole pomocí cyklu.
- Pro každý prvek zkontrolujte, zda se rovná hledanému prvku.
- Pokud se prvek rovná hledanému, vraťte `True`.
- Pokud se po průchodu celým polem funkce stále provádí, znamená to, že hledaný prvek v poli není. Vraťte `False`.
- Projděte pole pomocí cyklu.
- Vypište zprávu na základě hodnoty vrácené funkcí `search_element`.
Nyní, na základě výše uvedených kroků, zkuste sami napsat kód pro implementaci lineárního vyhledávání.
Podařilo se vám implementovat lineární vyhledávání? Doufám, že ano. Pokud ano, zkontrolujte, zda se váš kód shoduje s následujícím.
Pokud se vám to nepodařilo, nezoufejte. Podívejte se na kód níže a pochopte, jak jsme algoritmus implementovali. Určitě to zvládnete i sami.
## funkce pro vyhledávání def search_element(arr, n, element): ## iterace přes pole for i in range(n): ## kontrola aktuálního prvku s hledaným prvkem if arr[i] == element: ## vrácení True v případě shody return True ## prvek nebyl nalezen, proto se provede tento krok return False if __name__ == '__main__': ## inicializace pole, délky a prvku, který se má vyhledat arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 6 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "je nalezen") else: print(element_to_be_searched, "není nalezen")
Nejprve spusťte program s prvkem, který se v poli nachází, a poté s prvkem, který v poli není.
Časová složitost lineárního vyhledávání je O(n).
Dá se časová složitost ještě zmenšit pomocí jiného přístupu?
Ano, dá. Podívejme se jak.
Binární vyhledávání
Binární vyhledávací algoritmus vždy kontroluje prostřední prvek pole. Tento algoritmus funguje pouze na seřazených polích.
Algoritmus prochází polem a zkontroluje prostřední prvek. Pokud je hledaný prvek nalezen, program se zastaví. Pokud je prostřední prvek menší než hledaný prvek, vynechá levou část pole (včetně prostředního prvku). Pokud je naopak prostřední prvek větší než hledaný prvek, vynechá pravou část pole (včetně prostředního prvku).
V každé iteraci binární vyhledávání zmenšuje oblast, ve které hledá prvek. Počet kontrol je tedy menší než u lineárního vyhledávání.
Pro lepší pochopení si binární vyhledávání ilustrujeme.
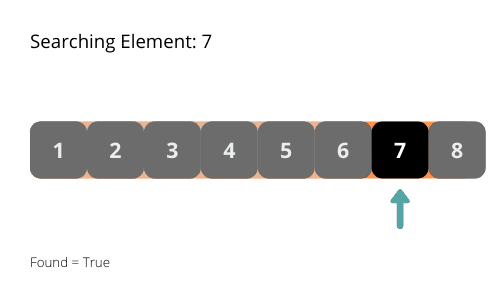
Časová složitost binárního vyhledávání je O(log n). V každé iteraci se délka oblasti prohledávání zmenší na polovinu. Rychlost se tedy snižuje exponenciálně.
Implementace binárního vyhledávání
Nejprve si představíme kroky potřebné pro implementaci binárního vyhledávání, a potom se podíváme na samotný kód. Zde jsou kroky potřebné k dokončení implementace binárního vyhledávání:
- Inicializujte pole s prvky (například s vašimi oblíbenými čísly).
- Napište funkci nazvanou `search_element`, která přijímá tři argumenty: seřazené pole, jeho délku a prvek, který hledáme.
- Funkce `search_element(sorted_arr, n, element)`:
- Inicializujte proměnnou `i` jako index pro procházení polem.
- Dále inicializujte dvě proměnné, které budou ohraničovat oblast hledání: `start` a `end`, představující indexy.
- Opakujte cyklus, dokud `i` není menší než délka pole.
- Vypočtěte střední index aktuální oblasti hledání jako `(start + end) // 2`.
- Zkontrolujte, zda se prvek na středním indexu rovná hledanému prvku.
- Pokud ano, vraťte `True`.
- Pokud je prvek na středním indexu menší než hledaný prvek, posuňte začátek oblasti hledání na `middle + 1`.
- Pokud je prvek na středním indexu větší než hledaný prvek, posuňte konec oblasti hledání na `middle – 1`.
- Zvyšte hodnotu indexu pole `i`.
- Pokud se po průchodu celým polem funkce stále provádí, znamená to, že hledaný prvek v poli není. Vraťte `False`.
- Vypište zprávu na základě hodnoty vrácené funkcí `search_element`.
Zkuste nyní sami napsat kód, podobně jako u lineárního vyhledávání.
…
Podařilo se vám napsat kód?
Pokud ano, porovnejte ho s kódem uvedeným níže. Pokud ne, nezoufejte a pochopte implementaci z kódu níže.
## funkce pro vyhledávání def search_element(sorted_arr, n, element): ## index pole pro iteraci i = 0 ## proměnné pro sledování oblasti vyhledávání ## inicializace s počátečním a koncovým indexem start = 0 end = n - 1 ## iterace přes pole while i < n: ## získání indexu prostředního prvku middle = (start + end) // 2 ## kontrola prostředního prvku s hledaným prvkem if sorted_arr[middle] == element: ## vrácení True, pokud je prvek v poli return True elif sorted_arr[middle] < element: ## posunutí počátečního indexu oblasti vyhledávání doprava start = middle + 1 else: ## posunutí koncového indexu oblasti vyhledávání doleva end = middle - 1 i += 1 return False if __name__ == '__main__': ## inicializace pole, délky a prvku, který se má vyhledat arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 9 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "je nalezen") else: print(element_to_be_searched, "není nalezen")
Vyzkoušejte kód s různými případy: když je prvek v poli přítomen, a když přítomen není.
Závěr
Binární vyhledávání je mnohem efektivnější než lineární vyhledávání. Pro binární vyhledávání je však nutné mít pole seřazené, což u lineárního vyhledávání není potřeba. Třídění však také zabere nějaký čas. Použitím efektivních třídicích algoritmů dosáhneme dobré kombinace s binárním vyhledáváním.
Nyní máte základní přehled o nejpoužívanějších vyhledávacích algoritmech v jazyce Python.
Dále se můžete seznámit s některými populárními vyhledávacími programy s vlastním hostingem.
Veselé kódování 🙂 🧑💻