Excel má vestavěné funkce, které můžete použít k zobrazení vašich kalibračních dat a vypočítat linii nejlépe vyhovující. To může být užitečné, když píšete zprávu z chemické laboratoře nebo programujete korekční faktor do zařízení.
V tomto článku se podíváme na to, jak pomocí Excelu vytvořit graf, vykreslit lineární kalibrační křivku, zobrazit vzorec kalibrační křivky a poté nastavit jednoduché vzorce pomocí funkcí SLOPE a INTERCEPT pro použití kalibrační rovnice v Excelu.
Table of Contents
Co je to kalibrační křivka a jak je Excel užitečný při jejím vytváření?
Chcete-li provést kalibraci, porovnáte naměřené hodnoty zařízení (jako je teplota, kterou zobrazuje teploměr) se známými hodnotami nazývanými standardy (jako jsou body tuhnutí a varu vody). To vám umožní vytvořit řadu párů dat, které pak použijete k vytvoření kalibrační křivky.
Dvoubodová kalibrace teploměru pomocí bodů tuhnutí a varu vody by měla dva datové páry: jeden z dat, kdy je teploměr umístěn do ledové vody (32 °F nebo 0 °C) a jeden do vroucí vody (212 °F). nebo 100 °C). Když vykreslíte tyto dva datové páry jako body a nakreslíte mezi nimi čáru (kalibrační křivku), pak za předpokladu, že odezva teploměru je lineární, můžete vybrat jakýkoli bod na čáře, který odpovídá hodnotě zobrazené teploměrem. mohl najít odpovídající „skutečnou“ teplotu.
Čára tedy za vás v podstatě vyplňuje informace mezi dvěma známými body, abyste si mohli být přiměřeně jisti při odhadu skutečné teploty, když teploměr ukazuje 57,2 stupňů, ale když jste nikdy nenaměřili „normu“, která odpovídá to čtení.
Excel má funkce, které vám umožňují graficky vykreslit páry dat do grafu, přidat spojnici trendu (kalibrační křivku) a zobrazit rovnici kalibrační křivky v grafu. To je užitečné pro vizuální zobrazení, ale můžete také vypočítat vzorec čáry pomocí funkcí SLOPE a INTERCEPT aplikace Excel. Když tyto hodnoty zadáte do jednoduchých vzorců, budete moci automaticky vypočítat „skutečnou“ hodnotu na základě jakéhokoli měření.
Podívejme se na příklad
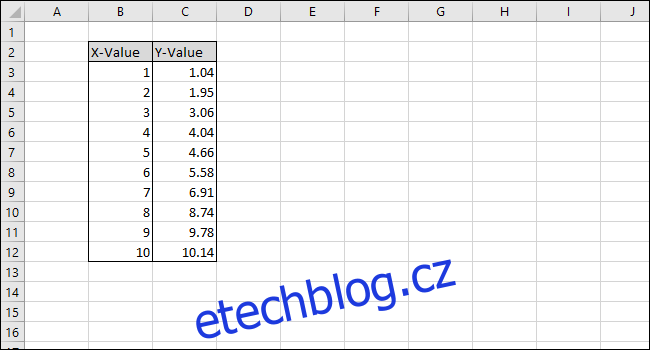
Pro tento příklad vytvoříme kalibrační křivku ze série deseti párů dat, z nichž každý se skládá z hodnoty X a hodnoty Y. Hodnoty X budou našimi „standardy“ a mohly by představovat cokoli od koncentrace chemického roztoku, kterou měříme pomocí vědeckého přístroje, až po vstupní proměnnou programu, který řídí odpalovací stroj na mramor.
Hodnoty Y budou „odpovědi“ a budou představovat údaje poskytnuté přístrojem při měření každého chemického roztoku nebo změřenou vzdálenost, jak daleko od odpalovacího zařízení dopadl mramor pomocí každé vstupní hodnoty.
Poté, co graficky znázorníme kalibrační křivku, použijeme funkce SLOPE a INTERCEPT k výpočtu vzorce kalibrační přímky a určíme koncentraci „neznámého“ chemického roztoku na základě údajů z přístroje nebo rozhodneme, jaký vstup bychom měli dát programu, aby mramor dopadne v určité vzdálenosti od odpalovacího zařízení.
První krok: Vytvořte svůj graf
Náš jednoduchý příklad tabulky se skládá ze dvou sloupců: X-hodnota a Y-hodnota.
Začněme výběrem dat k vykreslení do grafu.
Nejprve vyberte buňky sloupce ‚X-Value‘.
Nyní stiskněte klávesu Ctrl a poté klikněte na buňky sloupce Y-Value.
Přejděte na kartu „Vložit“.
Přejděte do nabídky „Grafy“ a v rozevíracím seznamu „Rozptyl“ vyberte první možnost.
Vyberte sérii kliknutím na jeden z modrých bodů. Jakmile vyberete, Excel načrtne body, které budou obrysy.
Klikněte pravým tlačítkem na jeden z bodů a poté vyberte možnost „Přidat trendovou linii“.
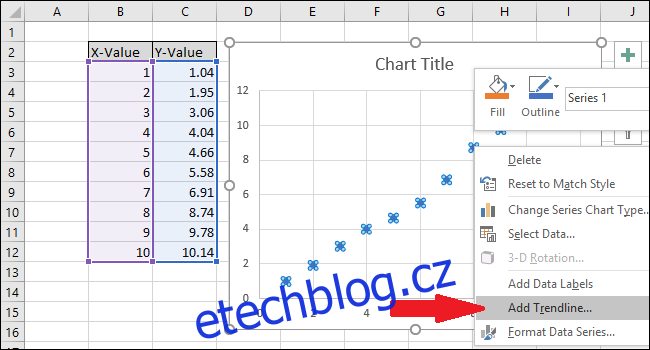
Na grafu se objeví přímka.
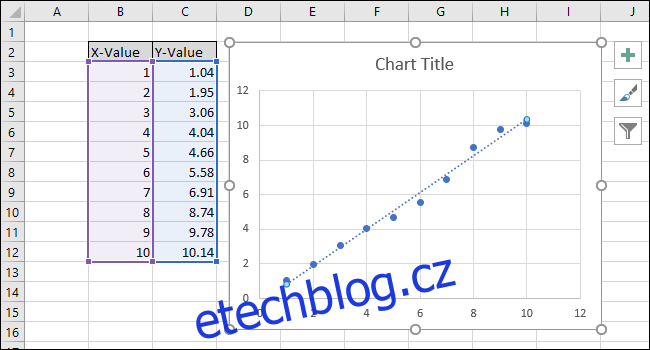
Na pravé straně obrazovky se zobrazí nabídka „Formát trendové linie“. Zaškrtněte políčka vedle položek „Zobrazit rovnici v grafu“ a „Zobrazit v grafu druhou mocninu“. Hodnota R-squared je statistika, která vám říká, jak přesně čára odpovídá datům. Nejlepší hodnota R-squared je 1 000, což znamená, že každý datový bod se dotýká čáry. Jak se rozdíly mezi datovými body a přímkou zvětšují, hodnota r-kvadrát klesá, přičemž 0,000 je nejnižší možná hodnota.
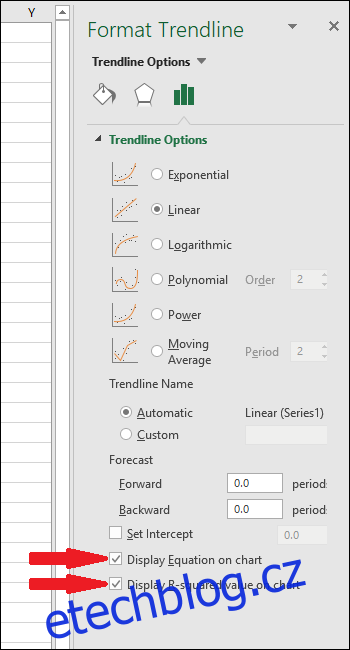
V grafu se objeví rovnice a statistika R-kvadrát trendové čáry. Všimněte si, že korelace dat je v našem příkladu velmi dobrá, s hodnotou R-kvadrát 0,988.
Rovnice je ve tvaru „Y = Mx + B“, kde M je sklon a B je průsečík přímky na ose y.
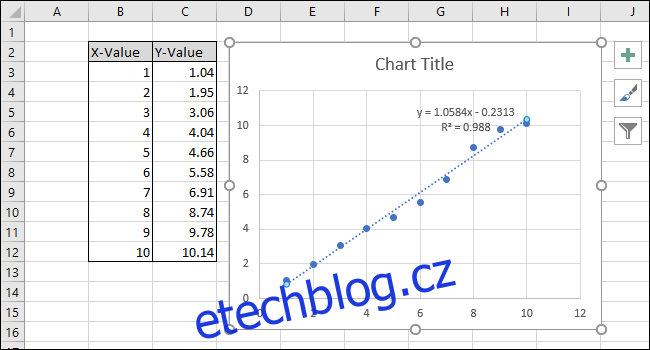
Nyní, když je kalibrace dokončena, pojďme pracovat na přizpůsobení grafu úpravou nadpisu a přidáním nadpisů os.
Chcete-li změnit název grafu, klikněte na něj a vyberte text.
Nyní zadejte nový název, který popisuje graf.
Chcete-li přidat nadpisy na osu x a osu y, nejprve přejděte na Nástroje grafu > Návrh.

Nyní přejděte na Názvy os > Primární horizontální.

Chcete-li přejmenovat název osy, nejprve vyberte text a poté zadejte nový název.
Nyní přejděte na Názvy os > Primární vertikální.
Zobrazí se název osy.
Přejmenujte tento název výběrem textu a zadáním nového názvu.
Váš graf je nyní kompletní.
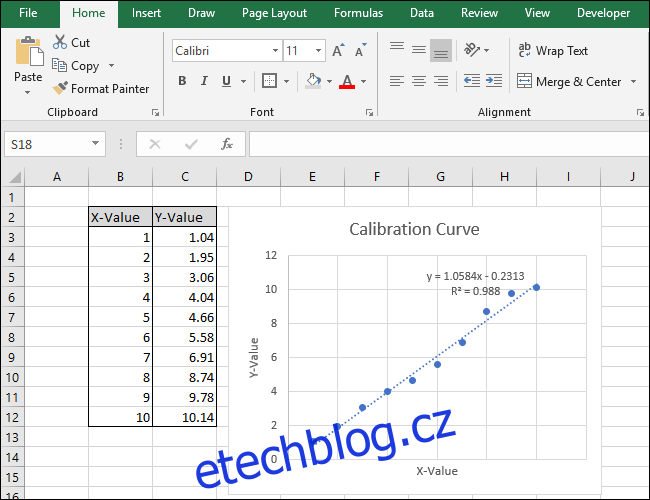
Krok 2: Vypočítejte přímkovou rovnici a statistiku R-squared
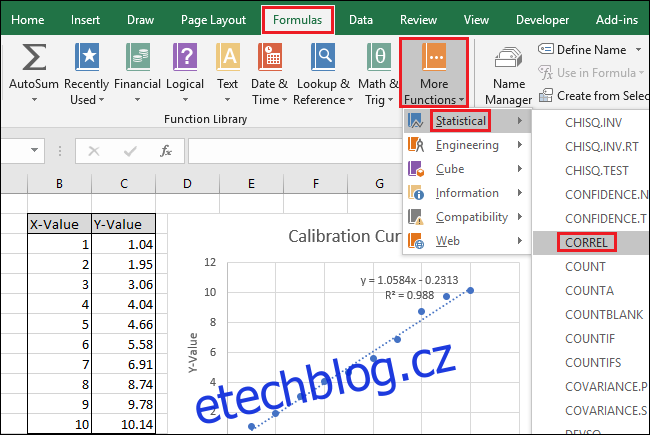
Nyní pojďme vypočítat rovnici přímky a statistiku R-squared pomocí vestavěných funkcí SLOPE, INTERCEPT a CORREL v Excelu.
Do našeho listu (v řádku 14) jsme přidali názvy pro tyto tři funkce. Vlastní výpočty provedeme v buňkách pod těmito názvy.
Nejprve spočítáme SLOPE. Vyberte buňku A15.
Přejděte na Vzorce > Další funkce > Statistické > SLOPE.
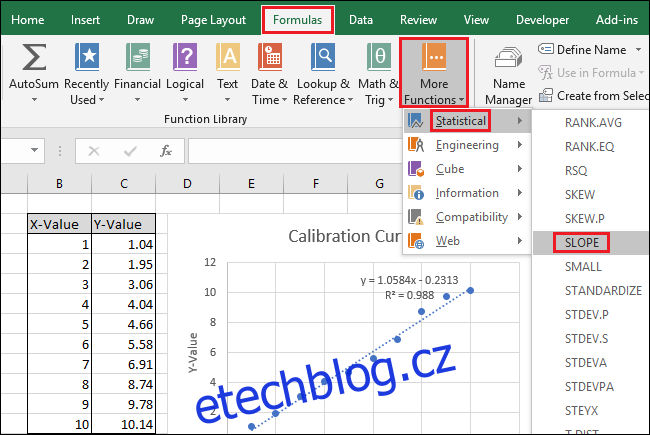
V poli „Known_xs“ vyberte nebo zadejte buňky sloupce X-Value. Ve funkci SLOPE záleží na pořadí polí ‚Known_ys‘ a ‚Known_xs‘.
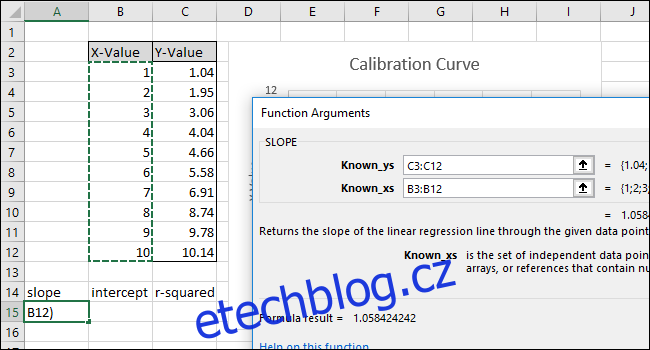
Klikněte na „OK“. Konečný vzorec na řádku vzorců by měl vypadat takto:
=SLOPE(C3:C12;B3:B12)
Všimněte si, že hodnota vrácená funkcí SLOPE v buňce A15 odpovídá hodnotě zobrazené v grafu.
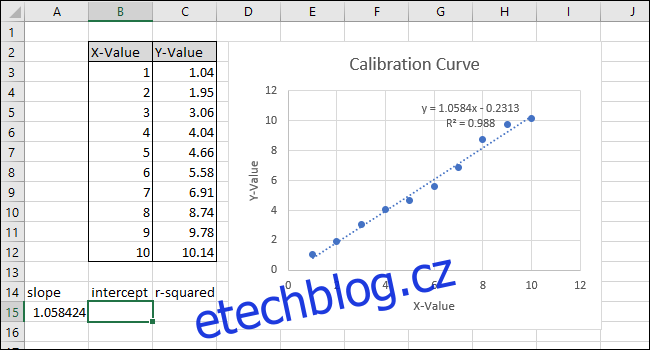
Dále vyberte buňku B15 a poté přejděte na Vzorce > Další funkce > Statistika > INTERCEPT.
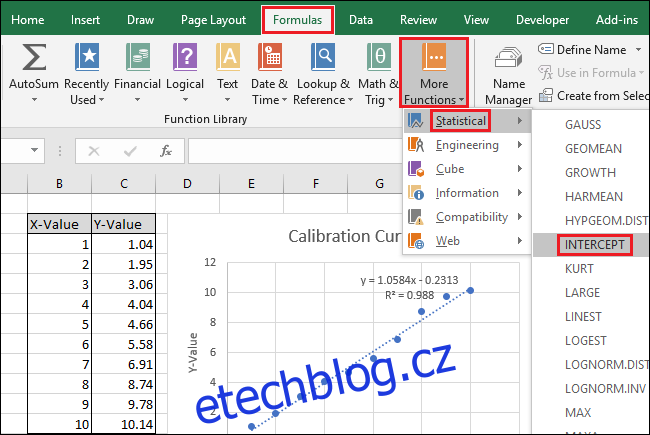
Vyberte nebo zadejte do buněk sloupce X-Value pole „Known_xs“. Ve funkci INTERCEPT záleží také na pořadí polí ‚Known_ys‘ a ‚Known_xs‘.
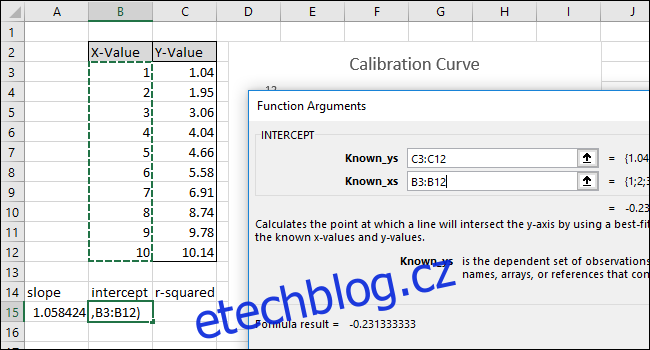
Klikněte na „OK“. Konečný vzorec na řádku vzorců by měl vypadat takto:
=INTERCEPT(C3:C12;B3:B12)
Všimněte si, že hodnota vrácená funkcí INTERCEPT odpovídá průsečíku y zobrazenému v grafu.
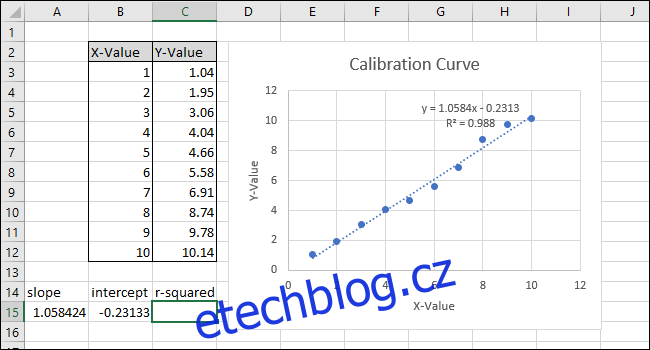
Dále vyberte buňku C15 a přejděte na Vzorce > Další funkce > Statistika > KOREL.
Vyberte nebo zadejte druhý ze dvou rozsahů buněk pro pole „Array2“.
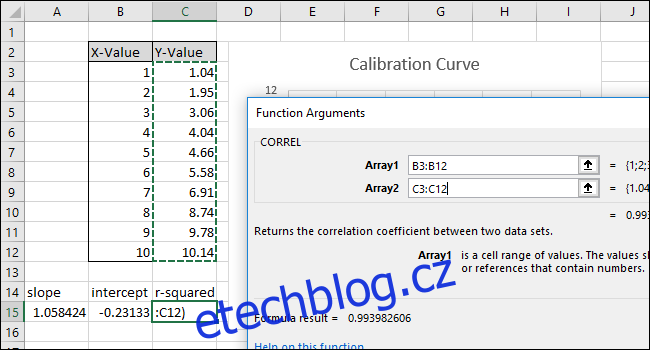
Klikněte na „OK“. Vzorec by měl na řádku vzorců vypadat takto:
=CORREL(B3:B12,C3:C12)
Všimněte si, že hodnota vrácená funkcí CORREL neodpovídá hodnotě „r-squared“ v grafu. Funkce CORREL vrátí „R“, takže ji musíme umocnit, abychom vypočítali „R-squared“.
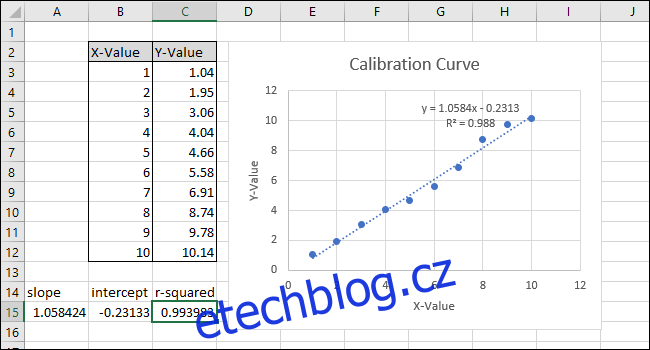
Klikněte do panelu funkcí a přidejte „^2“ na konec vzorce, abyste odmocnili hodnotu vrácenou funkcí CORREL. Hotový vzorec by nyní měl vypadat takto:
=CORREL(B3:B12,C3:C12)^2
Stiskněte Enter.
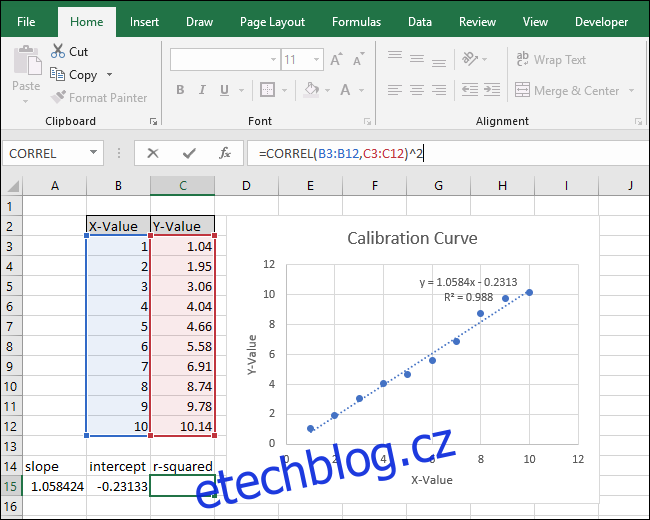
Po změně vzorce se hodnota „R-squared“ nyní shoduje s hodnotou zobrazenou v grafu.
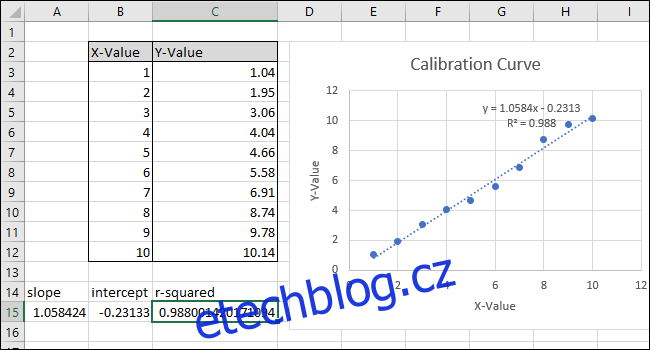
Krok tři: Nastavte vzorce pro rychlý výpočet hodnot
Nyní můžeme pomocí těchto hodnot v jednoduchých vzorcích určit koncentraci onoho „neznámého“ roztoku nebo jaký vstup máme zadat do kódu, aby kulička přeletěla určitou vzdálenost.
Tyto kroky nastaví vzorce potřebné k tomu, abyste mohli zadat hodnotu X nebo Y a získat odpovídající hodnotu na základě kalibrační křivky.
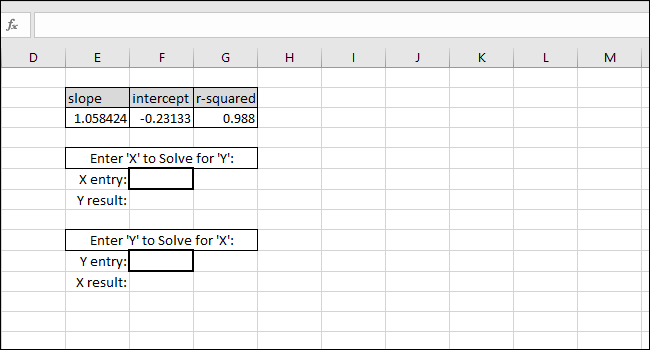
Rovnice přímky nejlepší shody je ve tvaru „hodnota Y = SLOPE * hodnota X + INTERCEPT“, takže řešení pro „hodnotu Y“ se provádí vynásobením hodnoty X a SLOPE a poté přidání INTERCEPT.
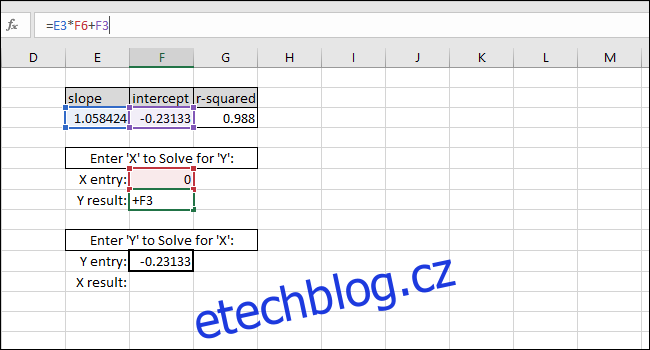
Jako příklad uvedeme nulu jako hodnotu X. Vrácená hodnota Y by se měla rovnat INTERCEPT čáry, která nejlépe odpovídá. Odpovídá, takže víme, že vzorec funguje správně.
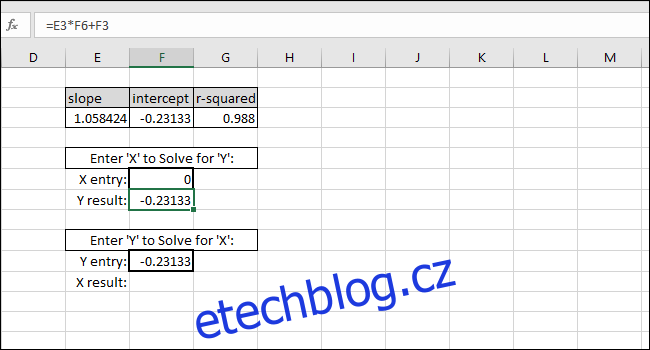
Řešení pro hodnotu X na základě hodnoty Y se provádí odečtením INTERCEPT od hodnoty Y a vydělením výsledku SLOPE:
X-value=(Y-value-INTERCEPT)/SLOPE
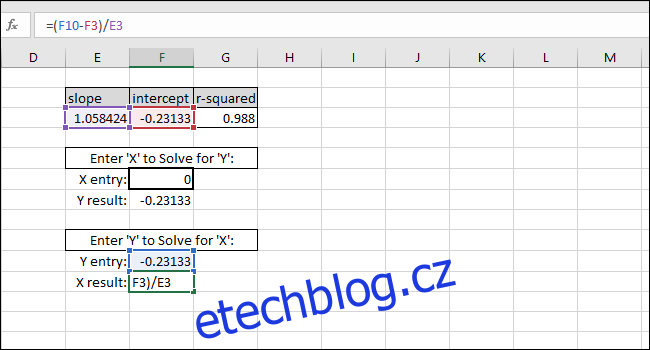
Jako příklad jsme použili INTERCEPT jako hodnotu Y. Vrácená hodnota X by měla být rovna nule, ale vrácená hodnota je 3.14934E-06. Vrácená hodnota není nula, protože jsme při psaní hodnoty nedopatřením zkrátili výsledek INTERCEPT. Vzorec však funguje správně, protože výsledek vzorce je 0,00000314934, což je v podstatě nula.
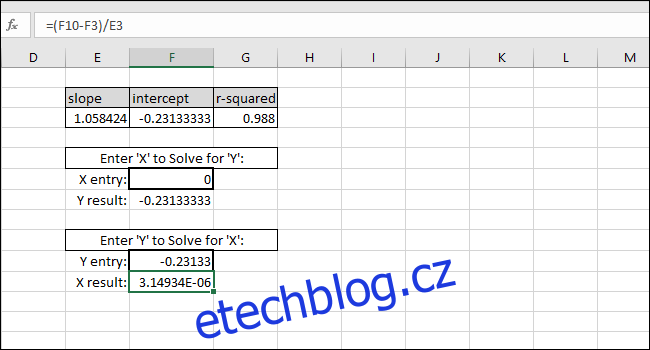
Do první buňky s tlustým okrajem můžete zadat libovolnou hodnotu X a Excel automaticky vypočítá odpovídající hodnotu Y.
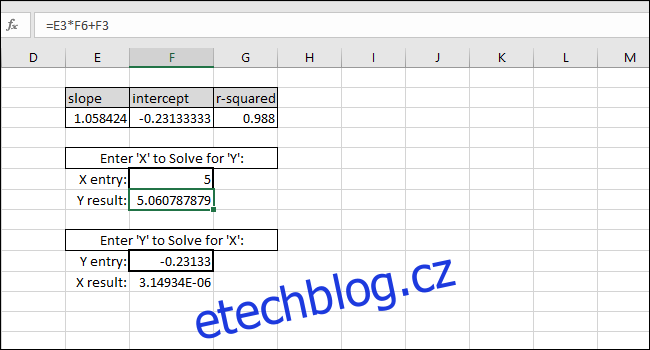
Zadáním libovolné hodnoty Y do druhé buňky s tlustým okrajem získáte odpovídající hodnotu X. Tento vzorec je to, co byste použili k výpočtu koncentrace tohoto roztoku nebo jaký vstup je potřeba k odpálení mramoru na určitou vzdálenost.
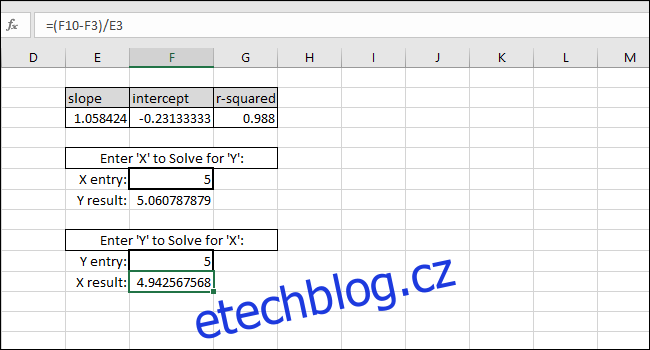
V tomto případě přístroj čte „5“, takže kalibrace by navrhla koncentraci 4,94 nebo chceme, aby kulička urazila pět jednotek vzdálenosti, takže kalibrace navrhuje zadat 4,94 jako vstupní proměnnou pro program ovládající odpalovací zařízení kuličky. Těmito výsledky si můžeme být přiměřeně jisti díky vysoké hodnotě R-squared v tomto příkladu.