Velký O Cheat Sheet: Vysvětleno s příklady Pythonu

Big O Analysis je technika pro analýzu a hodnocení účinnosti algoritmů.

To vám umožní vybrat nejúčinnější a škálovatelné algoritmy. Tento článek je Big O Cheat Sheet vysvětlující vše, co potřebujete vědět o Big O Notation.

Co je Big O analýza?

Big O Analysis je technika pro analýzu toho, jak dobře se algoritmy škálují. Konkrétně se ptáme, jak efektivní je algoritmus s rostoucí velikostí vstupu.

Efektivita je způsob využití systémových zdrojů při vytváření výstupu. Zdroje, o které nám jde především, jsou čas a paměť.

Proto při provádění analýzy Big O si klademe tyto otázky:

Jak se mění využití paměti algoritmem s rostoucí velikostí vstupu?

Jak se mění čas, který algoritmus potřebuje k vytvoření výstupu, když roste velikost vstupu?

Odpověď na první otázku je prostorová složitost algoritmu, zatímco odpovědí na druhou je jeho časová složitost. K vyjádření odpovědí na obě otázky používáme speciální notaci s názvem Big O Notation. To bude zahrnuto příště v Big O Cheat Sheet.

Předpoklady

Než se pustím kupředu, musím říci, že abyste z tohoto Big O Cheat Sheet vytěžili maximum, musíte trochu rozumět algebře. Navíc, protože budu uvádět příklady Pythonu, je také užitečné trochu porozumět Pythonu. Hloubkové porozumění je zbytečné, protože nebudete psát žádný kód.

Jak provést analýzu Big O

V této části se budeme zabývat tím, jak provést analýzu Big O.

Při provádění analýzy složitosti Big O je důležité si uvědomit, že výkon algoritmu závisí na tom, jak jsou strukturována vstupní data.

Například algoritmy řazení běží nejrychleji, když jsou data v seznamu již seřazena ve správném pořadí. To je nejlepší scénář pro výkon algoritmu. Na druhou stranu jsou stejné třídicí algoritmy nejpomalejší, když jsou data strukturována v opačném pořadí. To je ten nejhorší scénář.

Při provádění analýzy Big O uvažujeme pouze nejhorší scénář.

Analýza složitosti prostoru

Začněme tento Big O Cheat Sheet tím, že pokryjeme, jak provádět analýzu složitosti prostoru. Chceme zvážit, jak se přídavná paměť, kterou algoritmus používá, mění s tím, jak se vstup zvětšuje a zvětšuje.

Například funkce níže používá rekurzi ke smyčce z n na nulu. Má prostorovou složitost, která je přímo úměrná n. Důvodem je, že jak n roste, roste i počet volání funkcí v zásobníku volání. Má tedy prostorovou složitost O(n).

def loop_recursively(n):
    if n == -1:
        return
    else:
        print(n)
        loop_recursively(n - 1)

Lepší implementace by však vypadala takto:

def loop_normally(n):
    count = n
    while count >= 0:
        print(count)
        count =- 1

Ve výše uvedeném algoritmu vytvoříme pouze jednu další proměnnou a použijeme ji k zacyklení. Kdyby se n zvětšovalo a zvětšovalo, stále bychom používali pouze jednu další proměnnou. Proto má algoritmus konstantní prostorovou složitost označenou symbolem „O(1)“.

Porovnáním prostorové složitosti dvou výše uvedených algoritmů jsme dospěli k závěru, že smyčka while je účinnější než rekurze. To je hlavním cílem analýzy Big O: analyzovat, jak se algoritmy mění, když je spouštíme s většími vstupy.

Analýza časové složitosti

Při provádění analýzy časové složitosti nás nezajímá nárůst celkového času, který algoritmus zabere. Spíše nás znepokojuje nárůst podniknutých výpočetních kroků. Je to proto, že skutečný čas závisí na mnoha systémových a náhodných faktorech, které lze jen těžko zohlednit. Sledujeme tedy pouze růst výpočetních kroků a předpokládáme, že každý krok je stejný.

Chcete-li demonstrovat analýzu časové složitosti, zvažte následující příklad:

Předpokládejme, že máme seznam uživatelů, kde má každý uživatel své ID a jméno. Naším úkolem je implementovat funkci, která po přidělení ID vrátí jméno uživatele. Zde je návod, jak to můžeme udělat:

users = [
    {'id': 0, 'name': 'Alice'},
    {'id': 1, 'name': 'Bob'},
    {'id': 2, 'name': 'Charlie'},
]

def get_username(id, users):
    for user in users:
        if user['id'] == id:
            return user['name']
    return 'User not found'

get_username(1, users)

Když je uveden seznam uživatelů, náš algoritmus prochází celé pole uživatele, aby našel uživatele se správným ID. Když máme 3 uživatele, algoritmus provede 3 iterace. Když máme 10, provede 10.

Počet kroků je tedy lineárně a přímo úměrný počtu uživatelů. Náš algoritmus má tedy lineární časovou složitost. Náš algoritmus však můžeme vylepšit.

Předpokládejme, že namísto ukládání uživatelů do seznamu jsme je uložili do slovníku. Náš algoritmus pro vyhledání uživatele by pak vypadal takto:

users = {
    '0': 'Alice',
    '1': 'Bob',
    '2': 'Charlie'
}

def get_username(id, users):
     if id in users:
         return users[id]
     else:
         return 'User not found'

get_username(1, users)

Předpokládejme, že s tímto novým algoritmem máme v našem slovníku 3 uživatele; K získání uživatelského jména bychom provedli několik kroků. A předpokládejme, že máme více uživatelů, řekněme deset. Pro získání uživatele bychom provedli stejný počet kroků jako dříve. S rostoucím počtem uživatelů zůstává počet kroků k získání uživatelského jména konstantní.

Proto má tento nový algoritmus konstantní složitost. Nezáleží na tom, kolik uživatelů máme; počet provedených výpočetních kroků je stejný.

Co je to Big O Notation?

V předchozí části jsme diskutovali o tom, jak vypočítat prostorovou a časovou složitost Big O pro různé algoritmy. K popisu složitosti jsme použili slova jako lineární a konstantní. Dalším způsobem, jak popsat složitosti, je použít Big O Notation.

Big O Notation je způsob, jak znázornit prostorovou nebo časovou složitost algoritmu. Zápis je poměrně jednoduchý; je to O následované závorkami. Uvnitř závorek napíšeme funkci n reprezentující konkrétní složitost.

Lineární složitost je reprezentována n, takže bychom ji zapsali jako O(n) (čteno jako „O z n“). Konstantní složitost je reprezentována 1, takže bychom ji napsali jako O(1).

Existuje více složitostí, které probereme v další části. Obecně však platí, že chcete-li napsat složitost algoritmu, postupujte takto:

Pokuste se vyvinout matematickou funkci n, f(n), kde f(n) je množství použitého prostoru nebo výpočetních kroků následovaných algoritmem a n je vstupní velikost.

Vezměte nejdominantnější výraz v této funkci. Pořadí dominance různých členů od nejvíce dominantního po nejméně dominantní je následující: faktoriální, exponenciální, polynomiální, kvadratický, lineární, lineární, logaritmický a konstantní.

Odstraňte případné koeficienty z termínu.

Výsledkem je termín, který používáme v závorkách.

Příklad:

Zvažte následující funkci Pythonu:

users = [
    'Alice',
    'Bob',
    'Charlie'
]

def print_users(users):
    number_of_users = len(users)
    print("Total number of users:", number_of_users)

    for i in number_of_users:
        print(i, end=': ')
        print(user)

Nyní vypočítáme složitost algoritmu Big O Time.

Nejprve napíšeme matematickou funkci nf(n), která bude reprezentovat počet výpočetních kroků, které algoritmus provede. Připomeňme, že n představuje vstupní velikost.

Z našeho kódu funkce provede dva kroky: jeden vypočítá počet uživatelů a druhý vytiskne počet uživatelů. Poté pro každého uživatele provede dva kroky: jeden pro tisk indexu a druhý pro tisk uživatele.

Proto funkci, která nejlépe reprezentuje počet provedených výpočetních kroků, lze zapsat jako f(n) = 2 + 2n. Kde n je počet uživatelů.

Když přejdeme ke druhému kroku, vybereme nejdominantnější výraz. 2n je lineární člen a 2 je konstantní člen. Lineární je dominantnější než konstantní, takže zvolíme 2n, lineární člen.

Naše funkce je tedy nyní f(n) = 2n.

Posledním krokem je odstranění koeficientů. V naší funkci máme jako koeficient 2. Takže to eliminujeme. A funkce se stane f(n) = n. To je termín, který používáme v závorkách.

Proto je časová složitost našeho algoritmu O(n) neboli lineární složitost.

Různé velké O složitosti

Poslední sekce v našem Big O Cheat Sheetu vám ukáže různé složitosti a související grafy.

#1. Konstantní

Konstantní složitost znamená, že algoritmus používá konstantní množství prostoru (při provádění analýzy složitosti prostoru) nebo konstantní počet kroků (při provádění analýzy složitosti času). Toto je nejoptimálnější složitost, protože algoritmus nepotřebuje další prostor ani čas, protože vstup roste. Je tedy velmi škálovatelný.

Konstantní složitost je reprezentována jako O(1). Není však vždy možné napsat algoritmy, které běží v konstantní složitosti.

#2. Logaritmické

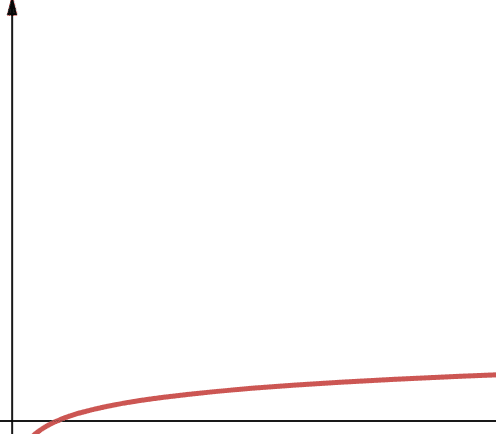
Logaritmická složitost je reprezentována pojmem O(log n). Je důležité poznamenat, že pokud logaritmický základ není specifikován v informatice, předpokládáme, že je 2.

Proto je log n log2n. Je známo, že logaritmické funkce nejprve rychle rostou a pak se zpomalují. To znamená, že se škálují a pracují efektivně se stále větším počtem n.

#3. Lineární

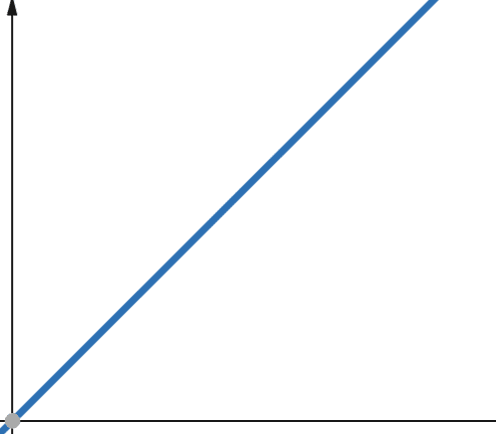
Pro lineární funkce, pokud se nezávislá proměnná změní o faktor p. Závislá proměnná se škáluje stejným faktorem p.

Proto funkce s lineární složitostí roste stejným faktorem jako vstupní velikost. Pokud se vstupní velikost zdvojnásobí, zvýší se i počet výpočetních kroků nebo využití paměti. Lineární složitost je reprezentována symbolem O(n).

#4. Linearitmické

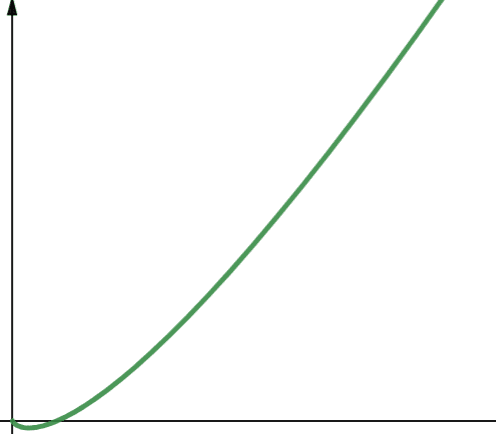
O (n * log n) představuje linearitmické funkce. Linearitmické funkce jsou lineární funkce vynásobené logaritmickou funkcí. Lineární funkce tedy poskytuje výsledky o něco větší než lineární funkce, když je log n větší než 1. Je to proto, že n se zvyšuje, když je vynásobeno číslem větším než 1.

Log n je větší než 1 pro všechny hodnoty n větší než 2 (pamatujte, že log n je log2n). Proto pro jakoukoli hodnotu n větší než 2 jsou lineární funkce méně škálovatelné než lineární funkce. Z nichž n je ve většině případů větší než 2. Lineární funkce jsou tedy obecně méně škálovatelné než logaritmické funkce.

#5. Kvadratický

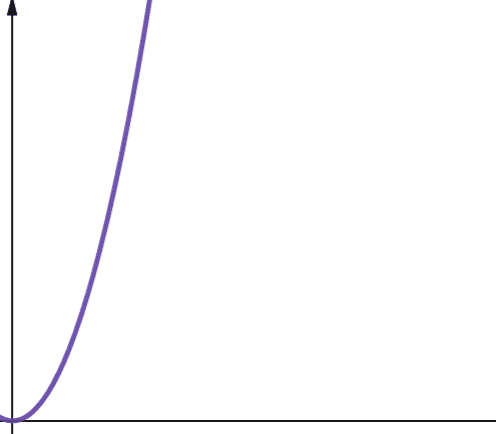
Kvadratickou složitost představuje O(n2). To znamená, že pokud se velikost vašeho vstupu zvýší 10krát, počet provedených kroků nebo využitý prostor se zvýší 102krát nebo 100! To není příliš škálovatelné, a jak můžete vidět z grafu, složitost vybuchne velmi rychle.

Kvadratická složitost vzniká v algoritmech, kde provádíte smyčku n-krát a pro každou iteraci provádíte smyčku nkrát znovu, například v Bubble Sort. I když to obecně není ideální, občas nemáte jinou možnost, než implementovat algoritmy s kvadratickou složitostí.

#6. Polynom

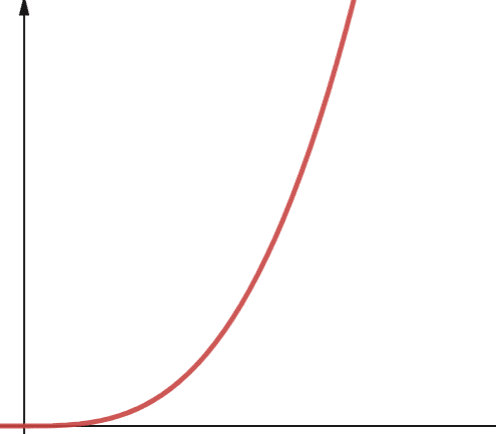
Algoritmus s polynomiální složitostí je reprezentován O(np), kde p je nějaké konstantní celé číslo. P představuje pořadí, ve kterém je n zvýšeno.

Tato složitost vzniká, když máte p počet vnořených smyček. Rozdíl mezi polynomiální složitostí a kvadratickou složitostí je kvadratický, je řádově 2, zatímco polynom má jakékoli číslo větší než 2.

#7. Exponenciální

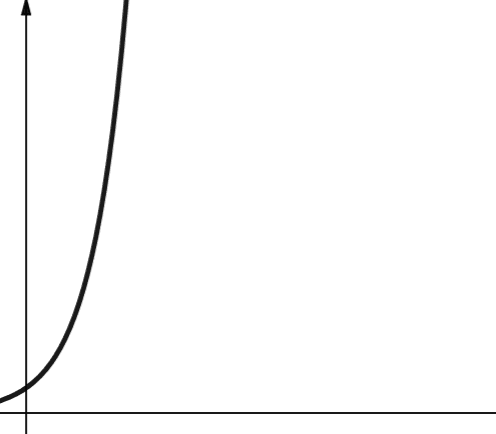
Exponenciální složitost roste ještě rychleji než polynomiální složitost. V matematice je výchozí hodnotou exponenciální funkce konstanta e (Eulerovo číslo). V informatice je však výchozí hodnota exponenciální funkce 2.

Exponenciální složitost je reprezentována symbolem O(2n). Když n je 0, 2n je 1. Ale když se n zvýší na 5, 2n se zvýší na 32. Zvýšení n o jednu zdvojnásobí předchozí číslo. Proto funkce exponenciály nejsou příliš škálovatelné.

#8. Faktorový

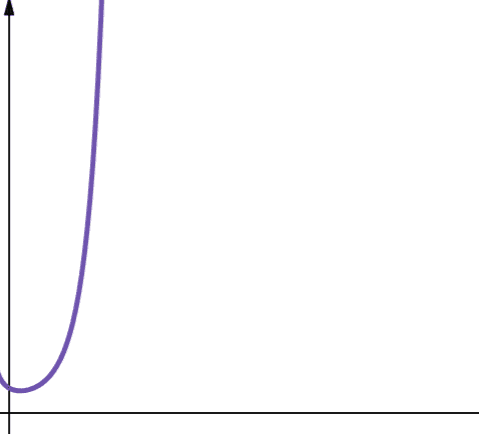
Faktorová složitost je reprezentována symbolem O(n!). Tato funkce také roste velmi rychle, a proto není škálovatelná.

Závěr

Tento článek se zabýval analýzou Big O a jak ji vypočítat. Probrali jsme také různé složitosti a diskutovali o jejich škálovatelnosti.

Dále si možná budete chtít procvičit analýzu Big O na třídicím algoritmu Python.