Co je to testování hypotéz a jak funguje?
Testování hypotéz je statistická metoda, kterou odborníci z různých oblastí, včetně soukromého i veřejného sektoru, využívají k formulování a ověřování pravděpodobných tvrzení o charakteristikách populace na základě vzorku dat.
Pokud jste se někdy zabývali analýzou dat nebo studiem charakteristik populace, pravděpodobně jste se s tímto klíčovým nástrojem statistické inference setkali.
Existuje mnoho přístupů, jak formulovat předpoklady, nicméně ne všechny poskytují srovnatelnou úroveň spolehlivosti.
Práce s daty, u kterých si nejste jisti jejich přesností, může představovat značné riziko pro vaši organizaci.
Testování hypotéz představuje efektivní strategii pro dosažení vyšší úrovně jistoty při analýze dat a je proto neocenitelným nástrojem v populační analýze.
V tomto článku se podrobně zaměříme na to, co testování hypotéz obnáší, jaké jsou jeho principy, výhody a oblasti použití.
Pojďme tedy bez zbytečného odkladu začít!
Co přesně je testování hypotéz?
Testování hypotéz představuje proces statistické inference, který analytikům umožňuje ověřit, zda data z vybraného vzorku dostatečně podporují určitou hypotézu o populaci, a na jejím základě vytvořit důvěryhodné předpoklady.
Díky této metodě mohou odborníci posoudit pravdivost hypotézy a určit, jak spolehlivé jsou na základě dostupných dat formulované závěry.
Zjednodušeně řečeno, jedná se o proces verifikace, který se opírá o statistické odvozeniny a umožňuje dospět k závěrům o celkové populaci na základě analýzy vzorku dat.
Pro analytiky je obvykle nemožné zkoumat vlastnosti či parametry kompletní populace. Díky testování hypotéz je však možné učinit informované předpovědi a rozhodnutí, založená na reprezentativním vzorku a jeho přesnosti.
Různé typy hypotéz
Existuje několik typů hypotéz, které se v rámci testování používají:
- Nulová hypotéza: Tato hypotéza předpokládá, že mezi zkoumanými proměnnými v datech vzorku neexistuje statisticky významný vztah nebo korelace, a případné odchylky jsou způsobeny náhodou.
- Alternativní hypotéza: Alternativní hypotéza prezentuje hlavní tezi a je v protikladu k nulové hypotéze. Ukazuje, že mezi proměnnými ve vzorku dat existuje významný vztah.
- Nedirektivní hypotéza: Jedná se o dvoustrannou hypotézu. Tvrdí, že mezi proměnnými existuje rozdíl, ale neurčuje směr tohoto rozdílu. Skutečná hodnota se liší od předpokládané, ale bez určení, zda je vyšší nebo nižší.
- Direktivní hypotéza: Tato hypotéza definuje vztah mezi proměnnými, a to i včetně směru tohoto vztahu. Jedna proměnná může mít vliv na druhou v konkrétním směru.
- Statistická hypotéza: Statistická hypotéza pomáhá analytikům posoudit, zda data a jejich hodnoty odpovídají určité hypotéze. Je užitečná pro formulování tvrzení a předpokladů o parametrech vzorku populace.
Dále se podíváme na metody testování hypotéz.
Metody testování hypotéz
Pro posouzení pravdivosti hypotézy je třeba nashromáždit důvěryhodné důkazy. V tomto procesu se před samotným hodnocením stanoví nulová a alternativní hypotéza. Testování hypotéz nabízí několik různých metod pro posouzení vhodnosti vzorkových dat. Při výběru metody je třeba vzít v úvahu charakter dat a velikost vzorku.
Testování normality
Jedná se o standardní metodu pro posouzení, zda mají data ve vzorku normální rozdělení. V procesu testování se ověřuje, zda se data seskupují rovnoměrně kolem průměru, nebo se od něj výrazně odchylují. V normálním rozdělení je pravděpodobnost výskytu hodnot nad a pod průměrem stejná. Výsledkem je zvonovitá křivka symetrická kolem průměru.
Z-test
Z-test se využívá, pokud data pocházejí z populace s normálním rozdělením. Testuje, zda se průměry dvou nezávislých populačních parametrů statisticky liší, a to za předpokladu, že známe rozptyl dat. Z-test je vhodný pro analýzu dat, kde je velikost vzorku větší než 30. Centrální limitní věta navíc uvádí, že se s rostoucí velikostí vzorku rozdělení vzorků blíží normálnímu, což podporuje vhodnost Z-testu.
T-test
T-test je aplikován, pokud je velikost vzorku omezená a data mají obvykle normální rozdělení. Používá se zejména tehdy, když je velikost vzorku menší než 30 a standardní odchylka parametru populace není známa. T-test se používá k odhadu intervalů spolehlivosti pro konkrétní populaci.
Chí-kvadrát test
Chí-kvadrát test je oblíbenou metodou pro posouzení vhodnosti a integrity rozdělení dat.
Zdroj: wikipedia.org
Tento test je vhodný pro situace, kdy je potřeba otestovat, zda se rozptyl vzorku shoduje s předpokládanou nebo známou hodnotou rozptylu populace. Existují různé varianty Chí-kvadrát testu, mezi nejběžnější patří test rozptylu a test nezávislosti.
Testování ANOVA

Analýza rozptylu (ANOVA) je statistická metoda, která slouží k porovnání průměrů více než dvou skupin dat. Umožňuje analyzovat vztah mezi závislou a nezávislou proměnnou v datech vzorku. Použití ANOVA je podobné Z-testu a T-testu, ale ty jsou omezeny pouze na porovnání dvou skupin.
Jak testování hypotéz funguje?
Při testování hypotéz se analyzují a porovnávají data náhodného vzorku. V průběhu testování se vzorová data používají k ověření nulové a alternativní hypotézy. Jak bylo již zmíněno, nulová a alternativní hypotéza se vzájemně vylučují, a během testu může být pravdivá pouze jedna z nich.
Může však nastat situace, kdy je nulová hypotéza zamítnuta, i když alternativní hypotéza není pravdivá.
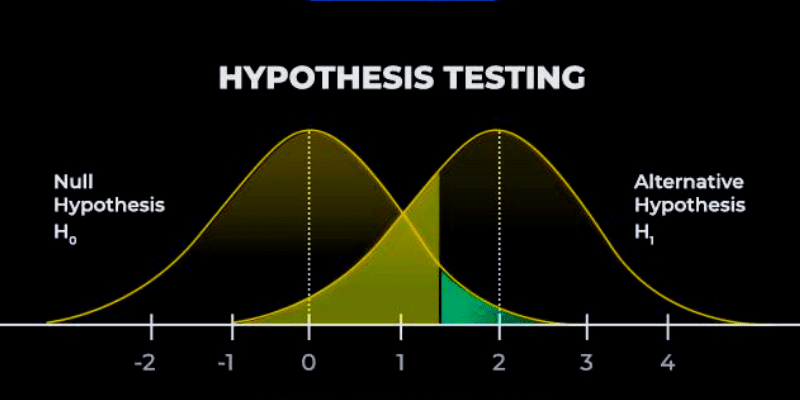
Zdroj: Analytics Steps
P-hodnota: Během testování se používá p-hodnota, která udává pravděpodobnost získání pozorovaných výsledků za předpokladu platnosti nulové hypotézy. P-hodnota také ukazuje pravděpodobnost výskytu chyby při zamítnutí nebo přijetí nulové hypotézy. Výsledná p-hodnota je v rozmezí 0 až 1, a porovnává se s hladinou významnosti (alfa).
Hladina významnosti představuje přijatelné riziko při zamítnutí nulové hypotézy. Je důležité si uvědomit, že výsledky testování hypotéz mohou vést ke dvěma typům chyb:
- Chyba typu 1: Nastane, když test zamítne nulovou hypotézu, i když je ve skutečnosti pravdivá.
- Chyba typu 2: Nastane, když test přijme nulovou hypotézu, přestože je ve skutečnosti nepravdivá.
Hodnoty, které vedou k zamítnutí nulové hypotézy, se nacházejí v kritické oblasti. Kritická hodnota je hranicí mezi kritickou oblastí a zbytkem rozdělení.
Kroky testování hypotéz
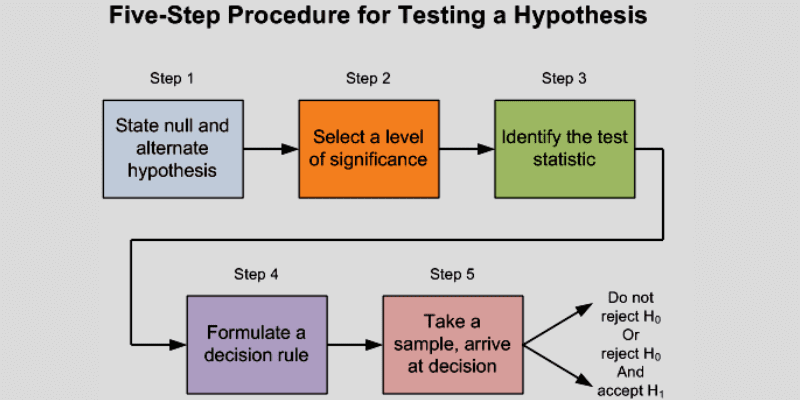
Zdroj: Medium
Testování hypotéz se skládá ze čtyř základních kroků:
- Definování hypotéz: Nejprve je nutné definovat nulovou a alternativní hypotézu, tak, aby mohla platit pouze jedna z nich. Například, nulová hypotéza by mohla tvrdit, že neexistuje rozdíl v průměrném BMI, zatímco alternativní hypotéza by tvrdila, že existuje významný rozdíl.
- Plánování: V dalším kroku je nutné sestavit plán analýzy. Je nutné získat relevantní data, a to takovým způsobem, aby byla vhodná pro testování zvolené hypotézy.
- Analýza vzorku dat: Dále následuje samotná analýza dat. Je nutné prověřit, zda vzorky dat jsou nezávislé a zda je jejich velikost dostatečná.
- Výpočet statistiky testu: V této fázi je nutné vypočítat statistiku testu a najít p-hodnotu. P-hodnota se určí za předpokladu, že nulová hypotéza je pravdivá.
- Vyhodnocení výsledku: V posledním kroku se vyhodnotí výsledek testování a na základě dat se rozhodne, zda zamítnout nulovou hypotézu, nebo ji přijmout.
Nyní se podíváme na výhody testování hypotéz.
Výhody testování hypotéz
Mezi hlavní výhody testování hypotéz patří:
- Umožňuje analyzovat sílu tvrzení, která souvisejí s rozhodnutím o datech.
- Vytváří spolehlivé prostředí pro rozhodování o vzorových datech.
- Umožňuje ověřit, zda jsou data použitá při testování hypotéz statisticky významná.
- Je nápomocné při hodnocení spolehlivosti a platnosti výsledků testů.
- Pomáhá extrapolovat data ze vzorku na větší populaci.
Příklady použití testování hypotéz
Testování hypotéz se využívá v mnoha odvětvích k ověření přesnosti vzorkových dat. Mezi příklady z reálného světa patří:
#1. Klinické testy
Testování hypotéz se často využívá v klinických studiích, aby se ověřila efektivita nových léků, léčebných postupů nebo lékařských metod. Na základě analýzy vzorkových dat se rozhoduje, zda je nová léčba účinná.
Například, lékař může prověřovat, zda nová léčba snižuje hladinu draslíku u pacientů. Před aplikací léčby se změří hladina draslíku u skupiny pacientů, a znovu se zkontroluje po ukončení léčby.

Dále se provede testování hypotéz. Nulová hypotéza (H0: Uafter = Ubefore) tvrdí, že léčba nemá vliv na hladinu draslíku. Alternativní hypotéza (Ha: Uafter < Ubefore) tvrdí, že léčba hladinu draslíku snižuje.
Pokud je p-hodnota nižší než hladina významnosti, lékař může dojít k závěru, že nová léčba skutečně snižuje hladinu draslíku.
#2. Výroba
Testování hypotéz pomáhá ve výrobních závodech při posuzování efektivity nových metod nebo technologií. Například, ve výrobním procesu se testuje hypotéza, zda nová metoda pomáhá snížit počet vadných výrobků. Předpokládejme, že počet vadných výrobků je 300 na jednu výrobní šarži.

Výrobce musí zjistit průměrný počet vadných výrobků před a po zavedení nové metody. Nulová hypotéza (H0: Uafter = Ubefore) tvrdí, že průměrný počet vadných výrobků po aplikaci nové metody je stejný jako dříve. Alternativní hypotéza (HA: Uafter ≠ Ubefore) tvrdí, že se počet vadných výrobků změnil.
Po testu se, pokud je p-hodnota nižší než hladina významnosti, usoudí, že se nová metoda promítla do změny počtu vadných produktů.
#3. Zemědělství
Testování hypotéz se používá ke zjištění, zda hnojiva a pesticidy ovlivňují růst a imunitu rostlin. Například, biologové testují, zda po aplikaci hnojiva naroste rostlina o více než 15 palců.

Biolog sleduje rostliny po dobu jednoho měsíce, aby shromáždil data. Nulová hypotéza (H0: U=15 palců) tvrdí, že hnojivo nemá vliv na průměrný růst rostliny. Alternativní hypotéza (HA: U> 15 palců) tvrdí, že hnojivo způsobuje zvýšení průměrného růstu rostliny. Po testu, pokud je p-hodnota nižší než hladina významnosti, biolog může dokázat, že hnojivo má vliv na růst.
Doporučené studijní materiály
#1. Statistika: Úvod krok za krokem od Udemy

Udemy nabízí kurz statistiky, který krok za krokem uvádí do základů statistiky, včetně testování hypotéz. Kurz zahrnuje příklady a lekce od zkušeného datového vědce ze společnosti Google a pomůže vám zvládnout intervaly spolehlivosti, testování hypotéz a další.
#2. Základní statistiky pro analýzu dat od Udemy
Tento kurz vám pomůže naučit se statistiku prostřednictvím praktických projektů a aktivit, a naučí vás testovat hypotézy, pracovat s rozdělením pravděpodobnosti, regresní analýzou a dalšími.
#3. Statistika pro datovou vědu a obchodní analýzu

Tento kurz nabízí Udemy a pomůže vám naučit se testování hypotéz. Pokrývá inferenční a popisnou statistiku, včetně regresní analýzy.
#4. Testování hypotéz od Jima Frosta
Tato kniha je intuitivním průvodcem, který pomáhá analytikům rozhodovat se na základě dat. Zabývá se principem testování hypotéz, intervaly spolehlivosti, p-hodnotami a hladinami významnosti.
#5. Testování hypotéz od Scotta Hartshorna
Kniha je jedinečná svým vizuálním zpracováním a je vhodná pro začátečníky. Jednoduše vysvětluje, jak testování hypotéz funguje a jaký je jeho význam. Nevyžaduje pokročilé znalosti statistiky.
Závěrem
Testování hypotéz pomáhá ověřit předpoklady a na základě tohoto procesu generovat statistická data. Je užitečné v mnoha odvětvích, od výroby a zemědělství až po klinické studie a IT. Tato metoda je přesná a pomáhá rozhodovat se na základě důvěryhodných dat. Prohlédněte si doporučené studijní zdroje a rozšiřte si své znalosti o obchodní analytice.